Свойства и признаки в геометрии

Признаки прямоугольника

У прямоугольника всего три основных признака:

По углу. Если один из углов параллелограмма равен 90 градусам, то параллелограмм является прямоугольником.
Если три угла четырехугольника равны 90 градусам, то такой четырехугольник является прямоугольником

Обратите внимание, что в этом случае нет необходимости доказывать, что перед нами параллелограмм. Достаточно знать значения углов четырехугольника.
По диагоналям: если диагонали параллелограмма равны, то такой параллелограмм является прямоугольником.

Обращайте внимание на то, к какой фигуре применяется признак, это имеет значение при доказательстве. В чем разница признака и свойства? Признак это отличие по которому можно выделить фигуру среди других

Как имя у человека. Вы видите знакомого, вспоминаете его имя и сразу знаете, что от него ожидать. А вот ожидания от человека это уже свойства. Свойства можно применять только после того, как вы доказали, что перед вами та или иная фигура. А для этого доказательства нам и необходимы признаки

В чем разница признака и свойства? Признак это отличие по которому можно выделить фигуру среди других. Как имя у человека. Вы видите знакомого, вспоминаете его имя и сразу знаете, что от него ожидать. А вот ожидания от человека это уже свойства. Свойства можно применять только после того, как вы доказали, что перед вами та или иная фигура. А для этого доказательства нам и необходимы признаки.

Что мы узнали?

Мы узнали, что такое параллелограмм. Поговорили о частных случаях параллелограмма, в том числе и о самом распространенном – прямоугольнике. Выделили свойства и признаки прямоугольника

Обратили внимание на то, что часть признаков действительно для любого четырехугольника, а часть только для параллелограмма

1. /10

   Вопрос 1 из 10

Различные формы выражения геометрических истин

Геометрические истины выражаются в форме аксиом, теорем, лемм и проблем или задач.

Аксиома есть истина, но своей очевидности не требующая доказательства.

Примерами истин, не требующих доказательства, могут послужить следующие аксиомы:

1. Целое равно сумме своих частей.

2. Целое больше своей части. Части меньше целого.

3. Две величины, равные одной и той же третьей, равны между собой.

4. Прибавив или вычтя из равных величин поровну, получим величины равные.

5. Прибавив или вычтя из равных величин не поровну, получим величины неравные.

6. Прибавив или вычтя из неравных величин поровну, получим величины неравные.

7. Сумма больших больше суммы меньших величин.

8. Однородная величина, которая не больше и не меньше другой, равна ей и т. д.

Теорема. Теоремой или предположением называется истина, требующая доказательства.

Доказательство есть совокупность рассуждений, делающих теорему очевидной.

Теорема доказывается при помощи аксиом.

Состав теоремы. Всякая теорема состоит из условия и заключения.

Условие называется иногда предположением, допущением, а заключение называют иногда следствием. Условие дано и потому получает иногда название данного.

Теорема называется обратной, если заключение делается условием, а условие или предположение заключением. В таком случае данная теорема называется прямою. Не всякая теорема имеет свою обратную.

Проблема или задача есть вопрос, разрешаемый при помощи теорем.

Лемма есть вспомогательная истина, облегчающая доказательство теоремы.

Роль признака в геометрии и примеры его применения

Признак в геометрии — это характеристика или свойство геометрической фигуры или объекта, которое позволяет отличать или описывать их. Признаки являются важным инструментом при изучении геометрических объектов и помогают в их классификации и сравнении.

Приведем некоторые примеры признаков и их применение:

Форма: признак, который описывает внешний вид геометрической фигуры. Например, круг, треугольник, прямоугольник, овал и т.д

Важно отметить, что форма может быть одним из признаков, позволяющих классифицировать фигуры.

Углы: признак, описывающий количество и величину углов в геометрической фигуре. Например, прямоугольник имеет 4 прямых угла, а правильный треугольник имеет 3 равных угла

Углы также могут быть использованы для классификации фигур.

Стороны: признак, описывающий количество и длину сторон в геометрической фигуре. Например, квадрат имеет 4 равные стороны, а треугольник может иметь стороны различной длины. Стороны могут помочь в определении типа фигуры.

Площадь: признак, описывающий размер поверхности геометрической фигуры. Площадь может использоваться для сравнения и классификации фигур по их размеру.

Объем: признак, описывающий объем трехмерной геометрической фигуры, такой как куб, сфера или цилиндр. Объем может быть использован для сравнения и классификации фигур по их объему.

Это только некоторые из множества признаков, которые используются в геометрии. Их сочетание и взаимодействие позволяют создавать точные описания и классификации геометрических объектов.

Что представляет собой свойство?

Рассматриваемое понятие может как предопределять совершенно уникальные характеристики предмета, так и формировать те или иные критерии для объединения соответствующего предмета в одну группу с какими-либо другими — возможно, и не похожими на него по сути. Особенно если близка их функциональность.

Например, с точки зрения применимости в машиностроении упругие пружины могут быть рассмотрены как детали, относящиеся к одной категории со столь же упругими шинами. По структуре это совершенно разные изделия. Но по свойству упругости и, как следствие, функциональности — очень близкие.

Свойства во многих случаях поддаются корректировке, то есть являются принципиально изменяемыми. Например, при размещении пружины в емкости с очень низкой температурой ее упругость может значительно снизиться, она станет хрупкой. С этой точки зрения свойство пружинистости может рассматриваться в данном случае как временный атрибут, который устойчив только при определенных условиях.

Равенства прямоугольных треугольников

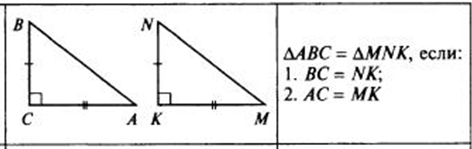
признаки

Два прямоугольных треугольника равны, если равны их катеты. То есть, по рисунку, если BC=NK, AC=MK, два треугольника, ABC и MNK равны.

по катету и прилежащему к нему острому углу

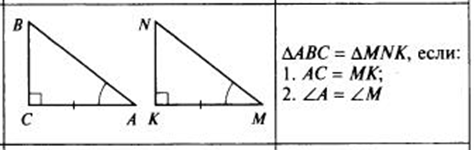
признаки

Если в прямоугольных треугольниках равны катеты и прилежащих к ним углы, такие треугольники равны. То есть, по рисунку, если AC=MK, углы C и K- прямые, углы A и M равны, такие прямоугольные треугольники равны.

по гипотенузе и острому углу

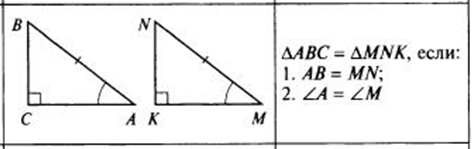
признаки

Два прямоугольных треугольника равны, если равны гипотенузы и острые углы. Например, по рисунку, AB=MN, углы A и M равны.

по гипотенузе и катету

признаки

Если в прямоугольных треугольниках равны гипотенузы и катеты, то такие треугольники равны. То есть, гипотенуза AB в треугольнике ABC равна гипотенузе MN, а также катет AC в треугольнике ABC равен катету KM в треугольнике NKN. Поэтому признаку (по гипотенузе и катету) равны прямоугольные треугольники. ABC и MNK, на данном рисунке выше.

Суть свойств и признаков в геометрии

Геометрия – наука, изучающая фигуры, пространственные объекты и их свойства. Одним из основных понятий в геометрии являются свойства и признаки.

Свойства – это особенности геометрических фигур и пространственных объектов, которые можно выделить и описать. Они помогают понять и описать форму, размеры, положение и другие характеристики объектов в геометрии.

Существует множество свойств в геометрии. Некоторые из них включают:

1. Свойство равенства – две геометрические фигуры или стороны могут быть равными, если их размеры и формы совпадают.
2. Свойство подобия – две геометрические фигуры являются подобными, если их формы совпадают, но размеры отличаются в определенном отношении.
3. Свойство параллельности – две или более линии называются параллельными, если они никогда не пересекаются.
4. Свойство перпендикулярности – две линии перпендикулярны, если они пересекаются под прямым углом.
5. Свойство взаимного расположения – определяет, как объекты расположены относительно друг друга: внутри, вне или на границе.

Признаки – это характеристики или свойства фигур и объектов, которые позволяют их идентифицировать и классифицировать. Признаки в геометрии обычно определяют форму и размеры геометрических фигур.

Существует множество признаков в геометрии. Некоторые из них включают:

• Признак квадрата – все четыре стороны равны, а углы прямые.
• Признак прямоугольника – все четыре угла прямые.
• Признак треугольника – три стороны и три угла.
• Признак круга – все точки на границе круга равноудалены от центра.

Свойства и признаки в геометрии помогают устанавливать отношения между объектами, классифицировать фигуры и исследовать их особенности. Они являются основой для решения геометрических задач и развития геометрического мышления.

Образование геометрических протяжений движением

На линию можно смотреть так же, как на след, оставляемый движением точки, на поверхность как на след, оставляемый движением лини и на тело как на след, оставляемый движением поверхности. На этих соображениях основаны другие определения линии, поверхности и тела.

Линия есть геометрическое место движущейся точки.

Поверхность есть геометрическое место движущейся линии.

Тело есть геометрическое место движущейся поверхности.

Все предметы, рассматриваемые в природе, имеют три измерения. В ней нет ни точек, ни линий, ни поверхностей, а существуют только тела. Однако в геометрии рассматривают точки, линии и поверхности отдельно от тел. При этом некоторое приближенное наглядное представление о поверхности дает нам очень тонкая оболочка тела, наглядное представление о линии дает очень тонкая нить или волосок и о точке конец нити.

Применение свойств и признаков в геометрии

Свойства и признаки в геометрии играют важную роль при решении различных задач и построении геометрических фигур. Они позволяют нам определить различные характеристики фигур и использовать их для решения задач.

Одним из основных свойств фигур в геометрии является их форма – геометрическая фигура может быть прямоугольной, квадратной, треугольной, круглой и т. д. Форма фигуры определяется ее сторонами и углами.

Еще одним важным свойством фигур является их размер. Размер фигуры определяется ее сторонами и диаметром (для круга). Для решения задач на вычисление площади или периметра фигуры необходимо знать ее размеры.

Признаки фигур в геометрии могут помочь нам определить, является ли фигура особой или обладает какими-то специальными свойствами. Например, квадрат обладает таким признаком, как равенство всех его сторон и углов. Также признаки могут помочь нам классифицировать фигуры – разделить их на группы по определенным свойствам.

Свойства и признаки используются не только при изучении геометрии, но и в повседневной жизни. Например, зная свойства треугольника, мы можем построить крышу дома или определить, как расположены дороги и улицы на карте города.

В заключение, свойства и признаки в геометрии являются неотъемлемой частью изучения геометрических фигур. Они позволяют нам определить форму и размеры фигур, использовать их для решения задач и классифицировать фигуры по их свойствам.

Определение и роль свойства в геометрии

Свойства в геометрии могут быть разделены на две категории: базовые свойства и производные свойства. Базовые свойства являются фундаментальными и принимаются за аксиомы или определения. Примеры базовых свойств в геометрии включают равенство углов, параллельность, перпендикулярность и др. Производные свойства выводятся из базовых свойств с помощью определенных логических рассуждений или геометрических конструкций.

Свойства в геометрии играют важную роль при анализе и решении геометрических задач. Они позволяют делать выводы и устанавливать связи между геометрическими объектами, а также применять специальные методы и приемы для нахождения решений задач. Например, свойство перпендикулярности может быть использовано для построения прямоугольного треугольника, а свойство суммы углов треугольника позволяет доказать теорему об углах треугольника, равных 180 градусам.

Важно отметить, что свойства в геометрии относительны и могут изменяться в зависимости от особенностей геометрической системы или модели, используемой для изучения объектов. Кроме того, свойства могут быть связаны и с другими разделами математики, такими как алгебра или анализ, и играть роль в решении более общих математических задач

В заключение, свойства в геометрии являются ключевыми элементами для описания и анализа геометрических объектов. Они позволяют устанавливать отношения и делать выводы, что делает их неотъемлемой частью геометрии и инструментом для решения задач.

Определение и основные понятия

Геометрия — наука, изучающая пространственные и связанные с этим фигуры, их свойства и преобразования.

Свойства фигур — это характеристики, присущие определенной фигуре или объекту в геометрии. Они могут быть геометрическими (например, форма, размеры, углы) или арифметическими (например, площадь, периметр).

Признаки фигур — это специальные свойства, которые помогают идентифицировать или классифицировать фигуры. Например, у прямоугольника две пары равных противоположных сторон и все углы прямые — это его признаки.

Фигура — это пространственный объект, обладающий определенными свойствами и обычно описываемый геометрическими терминами.

Треугольник — это фигура, состоящая из трех отрезков (сторон), соединяющихся между собой. У треугольника есть три вершины, три угла и три стороны.

Четырехугольник — это фигура, состоящая из четырех отрезков (сторон). У четырехугольника есть четыре вершины, четыре угла и четыре стороны.

Многоугольник — это фигура, состоящая из конечного числа отрезков, которые образуют замкнутую ломаную линию. У многоугольника может быть любое количество сторон, вершин и углов.

Форма — это свойство фигуры, определяющее ее внешний вид или облик, отличающий фигуру от других объектов.

Размеры — это свойства фигуры, которые определяют ее габариты, такие как длина сторон, радиусы, диаметры и т. д.

Углы — это свойства фигуры, которые определяются пересечением двух прямых линий или сторон фигуры. Углы могут быть различных величин и форм, например, прямыми, острыми или тупыми.

Периметр — это сумма длин всех сторон фигуры.

Площадь — это мера поверхности, занимаемой фигурой. Обычно вычисляется с использованием формул, зависящих от типа фигуры.

Ориентация — это пространственное положение или направление фигуры. Ориентация может быть определена, например, по положению вершин или углов относительно друг друга.

Симметрия — это свойство фигуры, которое означает, что она может быть разделена на две или более равные части, которые зеркально симметричны относительно некоторой оси или точки.

Параллельность — это свойство фигур или сторон, которое означает, что они никогда не пересекаются и всегда сохраняют постоянное расстояние между собой.

Перпендикулярность — это свойство фигур или сторон, которое означает, что они образуют угол в 90 градусов друг с другом.

Признaки четырехугольников

признаки

— Eсли в четырехугольнике две стороны равны и параллельны, то такой четырехугольник — параллелограмм.

— Если в четырехугольнике стороны попарно равны, то такой четырехугольник — параллелограмм.

— Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то такой четырехугольник — параллелограмм.

ромба

признаки

— признак ромба — если в параллелограмме диагонали пересекаются под параллелограмм, такой параллелограмм — ромб

— признак ромба — если в параллелограмме диагонали — биссектрисы углов, такой параллелограмм — ромб.

— если в параллелограмме все стороны равны, такой параллелограмм — ромб.

прямоугольника

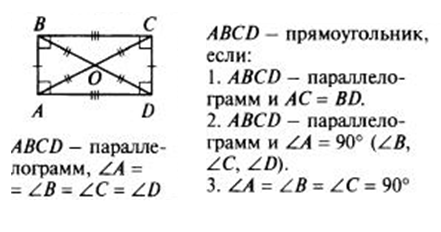
признаки

— параллелограмм является прямоугольником, если его диагонали равны. Например, на рисунке AC=BD.

— параллелограмм является прямоугольником. если один из углов равен 90 градусам.

— четырехугольник является прямоугольником, если три угла равны 90 градусам.

квадрата

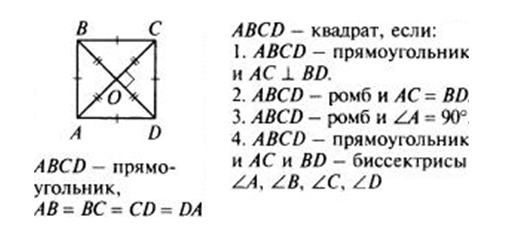
признак

— если в прямоугольнике диагонали перпендикулярны, такой прямоугольник — квадрат Например, на рисунке, ABCD — квадрат, если в прямоугольнике ABCD диагонали AB и CD перпендикулярны.

— если четырехугольник — ромб и у него хотя бы один угол равен 90 градусам. То есть, на рисунке. Угол A, например, равен 90 градусам, тогда ABCD — квадрат.

— если в прямоугольнике диагонали являются биссектрисами углов, такой прямоугольник — квадрат. Например, на рисунке: ABCD- прямоугольник, AC и BD — диагонали, и эти диагонали есть биссектрисы, тогда ABCD — квадрат.

трапеции

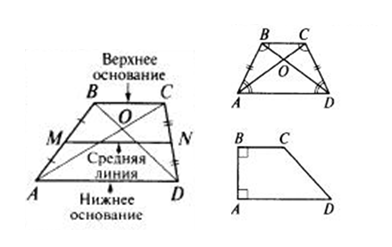
признаки

Признаками равнобокой трапеции и трапеции прямоугольной являются следующее:

— если в трапеции диагонали равны, то такая трапеция есть трапеция равнобокая.

— если в трапеции два угла равны 90 градусам, такая трапеция есть трапеция прямоугольная.

Линии

Линии разделяются на прямые, ломаные и кривые.

Прямая линия есть кратчайшее расстояние между двумя точками.

Сильно натянутая тонкая нить дает некоторое наглядное представление о прямой линии.

Всякую линию обозначают буквами, поставленными при ее точках. Чертеж 2 изображает прямую линию AB

Во всякой прямой линии обращают внимание на ее направление и величину

Направление прямой линии определяется ее положением.

Ломаная линия есть последовательное и непрерывное соединение нескольких прямых, имеющих неодинаковое направление.

Ломаная линия ABCD (черт. 3) составлена из прямых AB, BC, CD, имеющих неодинаковое направление.

Кривая линия есть такая, которая не может быть составлена из прямых.

Линия, изображенная на черт. 4, будет кривой линией.

Линия, составленная из прямых и кривых, называется иногда составной линией.

Чертеж (4, а) представляет такую составную линию.

 

Главные отличия свойств и признаков

Свойства, в геометрии — это характеристики геометрических объектов, которые остаются неизменными при различных преобразованиях. Они определяют геометрические особенности и связывают объекты с определенными характеристиками.

Признаки, в свою очередь, представляют собой особенности или свойства, которые позволяют идентифицировать определенный геометрический объект или делать выводы о его свойствах на основе имеющейся информации.

Основное отличие свойств от признаков заключается в их назначении:

• Свойства используются для описания геометрических объектов и определения их характеристик;
• Признаки предназначены для обнаружения и идентификации объектов на основе имеющейся информации о них.

Другое отличие свойств от признаков заключается в их изменяемости:

• Свойства остаются неизменными при различных преобразованиях, что позволяет использовать их для классификации и описания геометрических объектов;
• Признаки, в свою очередь, зависят от конкретного содержания исходной информации и могут изменяться в зависимости от того, какие параметры объекта мы рассматриваем.

Например, длина, площадь и объем являются свойствами геометрических объектов, так как они остаются неизменными при вращении или переносе объекта. В то же время, количество вершин или сторон является признаком фигуры, так как оно меняется в зависимости от конкретной фигуры.

Важно отметить, что свойства и признаки взаимосвязаны и взаимодополняют друг друга. Используя знание свойств объектов, мы можем выделить и использовать определенные признаки для их идентификации и описания

Что представляет собой признак?

С точки зрения науки под признаком следует понимать некоторое условие (совокупность условий) для идентификации какого-либо объекта либо отнесения его к той или иной категории. Например, пружина имеет такие признаки, как: спиралевидность, наличие металлической основы, наличие кольцеобразных витков на обоих торцах (что придает пружине устойчивость).

Признак — это постоянный атрибут какого-либо объекта. Принципиально он не может быть скорректирован. Если он будет существенно изменен, то объект станет другим, и его правомерно будет относить уже к другой категории. Например, если пружину в условиях воздействия очень высокой температуры растянуть — вследствие чего она перестанет быть спиралевидной,—то она превратится в проволоку.

Практическое применение свойств и признаков в геометрии

Свойства и признаки в геометрии играют важную роль в практическом решении различных задач. Они позволяют нам описывать, классифицировать и определять геометрические фигуры и объекты, а также проводить логические рассуждения на основе этих свойств.

Одним из практических применений свойств и признаков в геометрии является их использование при решении задач на построение геометрических фигур. Например, при задаче на построение треугольника с заданными углами и сторонами, мы можем использовать знание свойств треугольников (сумма углов треугольника равна 180 градусов, неравенство треугольника и т.д.) для определения геометрических конструкций и построения нужного треугольника.

Еще одним примером практического применения свойств и признаков в геометрии является нахождение неизвестных величин. Например, при задачах на нахождение площади, объема или других характеристик геометрических фигур, мы можем использовать свойства и признаки этих фигур для вычисления их характеристик. Например, при нахождении площади треугольника, мы можем использовать формулу площади треугольника для расчета площади на основе известных свойств треугольника (длины сторон и высоты).

Кроме того, знание свойств и признаков геометрических фигур позволяет проводить рассуждения и доказательства в геометрии. Например, при доказательстве теорем и утверждений, мы можем использовать свойства и признаки фигур, чтобы логически обосновать выводы и утверждения.

Таким образом, практическое применение свойств и признаков в геометрии широко распространено и включает в себя задачи на построение фигур, нахождение неизвестных величин и доказательства теорем. Знание этих свойств и признаков помогает нам решать геометрические задачи и проводить логические рассуждения на основе геометрических особенностей различных фигур.