Тема: общие сведения по геодезии. предмет геодезии

Картографическая проекция в геодезии: задачи и методы

Основной задачей картографической проекции является сохранение формы, углов и относительных расстояний на поверхности Земли при их отображении на плане или карте. Это позволяет производить точные измерения и проведение геодезических работ на основе карты.

Для решения задачи проецирования существует множество методов. Одним из самых распространенных является метод равноугольной цилиндрической проекции. В этом методе поверхность Земли представляется на плоскости цилиндрической формы, на который переносится каждая точка поверхности с сохранением углов и расстояний.

Другим распространенным методом является коническая проекция. В этом методе поверхность Земли представляется на плане конусообразной формы, который касается Земли по определенным меридианам или параллелям. Коническая проекция позволяет более точно отобразить определенную зону поверхности Земли.

Также существуют специальные методы проекций, разработанные для отображения территорий с крупномасштабными картами. Они позволяют подробно и точно изображать мелкие объекты и детали на местности.

Важно отметить, что при работе с картами необходимо учитывать искажения, связанные с проекцией. Они могут быть различными и варьируются в зависимости от выбранного метода проекции

Геодезисты должны быть внимательны и учитывать эти искажения при проведении работ.

Принципы геодезических проекций

Геодезические проекции используются для представления трехмерной поверхности Земли на плоскость.

Проекции обеспечивают сохранение определенных свойств геодезических объектов, таких как расстояния, углы и форма объектов,

и позволяют нам удобно работать с ними на карте. Вот несколько основных принципов, на которых строятся геодезические проекции:

1. Конформность

Конформная проекция с сохранением углов представляет поверхность Земли на плоскость таким образом,

что углы между касательными к проекциям геодезических кривых сохраняются. Это позволяет нам сохранять форму объектов

и регионов на карте, включая углы между дорогами, реками и границами.

2. Равновеликость

Равновеликая проекция сохраняет площади объектов на поверхности Земли.

Это означает, что соотношение площадей равно соотношению площадей их проекций на карту.

Это важно, когда важно обозначить площадь регионов или использовать карты для сравнения площадей разных областей. 3

Эквидистантность

3. Эквидистантность

Эквидистантная проекция сохраняет расстояния между точками на поверхности Земли.

Это позволяет нам измерять расстояния и строить прямые и плавные линии на карте.

Однако, в большинстве случаев, это достигается за счет искажения формы объектов.

4. Сжатие

При переводе трехмерной поверхности Земли на плоскость происходит сжатие или искажение объектов.

Это происходит из-за разности размера плоскости и поверхности Земли.

Чем ближе к полюсам, тем больше сжатие.

Для учета этого сжатия, различные виды проекций могут быть использованы,

что позволяет нам создавать карты с более точным представлением объектов на определенных широтах.

Понимание этих принципов позволяет геодезистам и картографам выбрать наиболее подходящую проекцию в зависимости от целей и ограничений.

Каждая геодезическая проекция имеет свои уникальные характеристики и может быть использована в различных ситуациях.

Примечание: Поиск наиболее подходящей проекции часто требует компромисса между основными принципами геодезических проекций,

то есть сохранение формы, конформность, равновеликость и эквидистантность.

Определение геодезических проекций

Геодезические проекции учитывают особенности Земли, такие как ее форма и размеры. Они представляют географическую информацию в виде карт, графиков или моделей, позволяя анализировать и использовать пространственные данные. Геодезические проекции широко применяются в различных областях, включая геодезию, картографию, географию, геологию и геофизику.

Таблица ниже приводит некоторые из основных типов геодезических проекций:

Тип проекции	Описание
Цилиндрическая проекция	Представляет поверхность Земли на цилиндре, который затем раскрывается в плоскость
Коническая проекция	Представляет поверхность Земли на конусе, который затем разворачивается в плоскость
Плоская проекция	Представляет поверхность Земли на плоскости
Полиэдральная проекция	Представляет поверхность Земли на множестве полиэдральных граней

Выбор конкретной геодезической проекции зависит от конкретной задачи и требуемой точности. Каждая проекция имеет свои преимущества и ограничения, которые необходимо учитывать при ее выборе.

1.1. Центральное проецирование

Проецирование (лат. Projicio – бросаю вперёд) – процесс получения изображения предмета (пространственного объекта) на какой-либо поверхности с помощью световых или зрительных лучей (лучей, условно соединяющих глаз наблюдателя с какой-либо точкой пространственного объекта), которые называются проецирующими.

Известны два метода проецирования: центральное  и параллельное.

Центральное проецирование заключается в проведении через каждую точку (А, В, С,…) изображаемого объекта и определённым образом выбранный центр проецирования (S) прямой линии (SA, SB, >… — проецирующего луча).

Рисунок 1.1 – Центральное проецирование

Введём следующие обозначения (Рисунок 1.1):

S – центр проецирования (глаз наблюдателя);
π₁ – плоскость проекций;

A, B, C – объекты проецирования – точки;

SA, SB – проецирующие прямые (проецирующие лучи).

Примечание: левой клавишей мыши можно переместить КРАСНУЮ точку в горизонтальной плоскости, при щелчке на точке левой клавишей мыши, изменится направление перемещения и её можно будет переместить по вертикали.

 Центральной проекцией точки называется точка пересечения проецирующей прямой, проходящей через центр проецирования и объект проецирования (точку), с плоскостью проекций.

Свойство 1. Каждой точке пространства соответствует единственная проекция, но каждой точке плоскости проекций соответствует множество точек пространства, лежащих на проецирующей прямой.

Докажем это утверждение.

На рисунке 1.1: точка А₁ – центральная проекция точки А на плоскости проекций π₁. Но эту же проекцию могут иметь все точки, лежащие на проецирующей прямой. Возьмём на проецирующей прямой SA точку С. Центральная проекция точки С (С₁) на плоскости проекций π₁ совпадает с проекцией точки А (А₁):

1. С ∈ SA;
2. SC ∩ π₁=C₁ → C₁ ≡ A₁.

Следует вывод, что по проекции точки нельзя судить однозначно о её положении в пространстве.

Чтобы устранить эту неопределенность, т.е. сделать чертеж обратимым, введём еще одну плоскость проекций (π₂) и ещё один центр проецирования (S₂) (Рисунок 1.2).

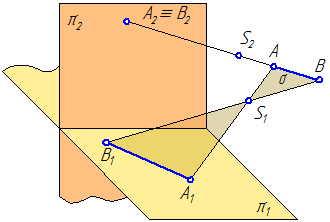
Рисунок 1.2 – Иллюстрация 1-го и 2-го свойств

Построим проекции точки А на плоскости проекций π₂. Из всех точек пространства только точка А имеет своими проекциями А₁ на плоскость π₁ и А₂ на π₂ одновременно. Все другие точки лежащие на проецирующих лучах будут иметь хотя бы одну отличную проекцию от проекций точки А (например, точка В).

Свойство 2. Проекция прямой есть прямая.

Докажем данное свойство.

Соединим точки А и В между собой (Рисунок 1.2). Получим отрезок АВ, задающий прямую. Треугольник ΔSAB задает плоскость, обозначенную через σ. Известно, что две плоскости пересекаются по прямой: σ∩π₁=А₁В₁, где А₁В₁ – центральная проекция прямой, заданной отрезком АВ.

Метод центрального проецирования – это модель восприятия изображения глазом, применяется главным образом при выполнении перспективных изображений строительных объектов, интерьеров, а также в кинотехнике и оптике. Метод центрального проецирования не решает основной задачи, стоящей перед инженером – точно отразить форму, размеры предмета, соотношение размеров различных элементов.

1.4. Прямоугольные проекции точки. Свойства ортогонального чертежа

1. Две прямоугольные проекции точки лежат на одной линии проекционной связи, перпендикулярной к оси проекций.

2. Две прямоугольные проекции точки однозначно определяют её положение в пространстве относительно плоскостей проекций.

Убедимся в справедливости последнего утверждения, для чего повернём плоскость π₁ в исходное положение (когда π₁⊥π₂). Для того, чтобы построить точку А необходимо из точек А₁ и А₂ восстановить проецирующие лучи, а фактически – перпендикуляры к плоскостям π₁и π₂, соответственно. Точка пересечения этих перпендикуляров фиксирует в пространстве искомую точку А. Рассмотрим ортогональный чертеж точки А (Рисунок 1.8).

Рисунок 1.8 – Построение эпюра точки

Введём третью (профильную) плоскость проекций π₃ перпендикулярную π₁ и π₂ (задана осью проекций π₂/π₃).

Расстояние от профильной проекции точки до вертикальной оси проекций А‘A₃ позволяет определить расстояние от точки А до фронтальной плоскости проекций π₂. Известно, что положение точки в пространстве можно зафиксировать относительно декартовой системы координат с помощью трёх чисел (координат) A(X_A; Y_A; Z_A) или относительно плоскостей проекций с помощью её двух ортогональных проекций (A₁=(X_A; Y_A); A₂=(X_A; Z_A)). На ортогональном чертеже по двум проекциям точки можно определить три её координаты и, наоборот, по трём координатам точки, построить её проекции (Рисунок 1.9, а и б).

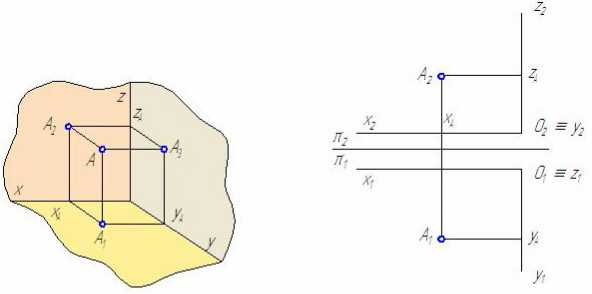а                                                                                   бРисунок 1.9 – Построение эпюра точки по её координатам

По расположению на эпюре проекций точки можно судить о её расположении в пространстве:

• если на эпюре горизонтальная проекция точки А — А₁ лежит под осью координат X , а фронтальная — А₂ – над осью X, то можно говорить, что точка А принадлежит 1-му квадранту;
• если на эпюре горизонтальная проекция точки А — А₁ лежит над осью координат X, а фронтальная — А₂ – под осью X, то точка А принадлежит 3-му квадранту;
• если на эпюре горизонтальная и фронтальная проекции точки А — А₁ и А₂ лежат над осью X, то точка А принадлежит 2-му квадранту;
• если на эпюре горизонтальная и фронтальная проекции точки А — А₁ и А₂ лежат под осью X, то точка А принадлежит 4-му квадранту;
• если на эпюре проекция точки совпадает с самой точкой, то значит – точка принадлежит плоскости проекций;
• точка, принадлежащая плоскости проекций или оси проекций (оси координат), называется точкой частного положения.

Для определения в каком квадранте пространства расположена точка, достаточно определить знак координат точки.

Зависимости квадранта положения точки и знаков координат

	X	Y	Z
I	+	+	+
II	+	—	+
III	+	—	—
IV	+	+	—

Способы изображения земной поверхности. Метод проекций в геодезии

_______На местности точки, линии, углы и контуры расположены в силу неровностей земной поверхности на возвышениях или впадинах. Так как возвышения и впадины являются пространственными формами, изобразить их на бумаге в виде плоской карты или плана достаточно непросто. Способы изображения земной поверхности на плоскости основываются на методе проекций.

_______При изучении действительной поверхности Земли точки местности проецируют отвесными линиями на поверхность земного эллипсоида. Так как уровенная поверхность радиусом до 20 км может быть заменена плоскостью, при относительно небольших площадях, точки местности проецируют на горизонтальную плоскость. Положение полученных проекций точек может быть определено координатами.

_______В результате перенесения точек на плоскость длины линий заменяют их горизонтальными проекциями, называемыми горизонтальными проложениями; пространственные углы заменяются плоскими, и вся фигура заменяется проекцией на горизонтальную плоскость (рис. 2).

Что такое геодезия

_______ Геодезия – это наука об измерениях на земной поверхности, выполняемых для изучения общей фигуры Земли, для составления планов и карт, для решения инженерных задач при изысканиях, проектировании, строительстве и эксплуатации инженерных сооружений.

_______В процессе своего развития геодезия разделилась на ряд самостоятельных научных дисциплин: высшую геодезию, топографию, инженерную геодезию, аэрофотогеодезию, картографию и космическую геодезию.

_______Высшая геодезия занимается определением фигуры и размеров всей Земли и значительных ее частей.

_______Топография занимается измерением и изображением на планах и картах земной поверхности.

_______Инженерная геодезия занимается вопросами геодезических работ при изысканиях, проектировании, строительстве и эксплуатации инженерных сооружений, при монтаже оборудования, при наблюдениях за вертикальными и горизонтальными смещениями инженерных сооружений и технологического оборудования.

_______Аэрофотогеодезия занимается изучением методов и средств создания топографических карт и планов по материалам фотографирования Земли.

_______Картография занимается изучением методов составления, издания и использования карт.

_______Космическая геодезия занимается обработкой измерений, полученных при помощи искусственных спутников Земли, орбитальных станций и межпланетных кораблей.

_______

Применение геодезических проекций

Геодезические проекции широко применяются в различных областях, где требуется точное и удобное изображение поверхности Земли на плоскости. Вот некоторые примеры применения геодезических проекций:

1. Картография: Геодезические проекции используются для создания карт и планов различных масштабов. Они позволяют передавать пространственные отношения между различными объектами на поверхности Земли точно и без искажений.

   

   

   

   

   

   

   

   

   

   

2. Геодезия и навигация: Геодезические проекции являются неотъемлемой частью геодезических измерений и навигации. Они помогают определять координаты точек и расстояния между ними на поверхности Земли с высокой точностью.

3. Аэрофотосъемка и спутниковая навигация: Геодезические проекции играют важную роль в обработке и интерпретации данных, полученных с помощью аэрофотосъемки и спутниковой навигации. Они помогают геодезистам и картографам получить точное цифровое изображение поверхности Земли.

4. Геоинформационные системы (ГИС): Геодезические проекции являются основой ГИС, которые используются для организации, анализа и визуализации геопространственных данных. Они позволяют легко соединять геоданные различных источников для дальнейшего исследования и принятия решений.

Это всего лишь несколько примеров применения геодезических проекций. Они находят применение в множестве других отраслей, таких как геология, геофизика, гидрология, геодезия строительства и многое другое.

Предмет геодезии. Понятие о форме и размерах Земли

_______Предметом геодезии является планета Земля. Общая площадь Земли – 510 млн. км2; 71% поверхности Земли – это моря и океаны, 29% – суша. При определении положения точек земной поверхности обычно относят их к общей фигуре Земли, которую называют геоидом.

_______Геоид – это геометрическое тело, ограниченное уровенной поверхностью.

_______Уровенная поверхность – поверхность, совпадающая с поверхностью воды в морях и океанах, которые находятся в спокойном состоянии, продолженная под материками.

_______Уровенная поверхность в каждой своей точке перпендикулярна к отвесной линии, проведенной через эту точку.

_______Фигура геоида в геометрическом отношении является весьма сложной, однако она очень близка к эллипсоиду вращения. Такой эллипсоид получается в результате вращения вокруг малой полуоси эллипса РQP₁Q₁ (рис. 1).

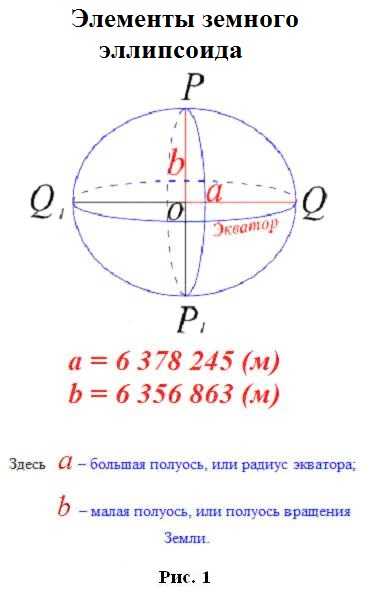_______Эти величины определяют форму и размеры Земли. В 1946 году были приняты размеры земного эллипсоида, вычисленные группой российских ученых под руководством профессора Ф.Н. Красовского. Эти размеры: а = 6378245 м и b = 6356863 м.

1.5. Задачи для самостоятельного решения

1. По эпюру определите положение точки относительно плоскостей проекций (Рисунок 1.11).

Рисунок 1.11

2. Достройте недостающие ортогональные проекции точек А, В, С на плоскости проекций π₁, π₂, π₃ (Рисунок 1.12).

Рисунок 1.12

3. Постройте проекции точки:

• Е, симметричной точке А относительно плоскости проекций π₁;
• F, симметричной точке В относительно плоскости проекций π₂;
• G, симметричной точке С относительно оси проекций π₂/π₁;
• H, симметричной точке D относительно биссекторной плоскости второго и четвертого квадрантов.

4. Постройте ортогональные проекции точки К, расположенной во втором квадранте и удаленной от плоскостей проекций π₁ на 40 мм, от π₂ — на 15 мм.

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.

Начало развития геодезических проекций

Первые попытки создания геодезических проекций были предприняты еще в древности. В Александрийской библиотеке, основанной в III веке до нашей эры, хранилось множество карт, созданных географами Египта, Греции и Рима. Они использовали различные геометрические методы для представления Земли на плоскости, но их проекции были примитивными и содержали значительные искажения.

Совершенствование геодезических проекций продолжалось в средние века. Особенно важным в этом процессе было усовершенствование методов картирования морей и окончательное определение формы Земли как геоида. Благодаря работам ученых таких как Клод Пернет, Меркатор и Гаусс был достигнут прогресс в создании более точных и неисказительных геодезических проекций.

С развитием науки и технологий в XIX и XX веках появилось большое количество различных типов геодезических проекций. Они были разработаны для различных целей, таких как навигация, аэрофотограмметрия, геодезия и геоинформационные системы.

Сегодня геодезические проекции широко используются во многих сферах человеческой деятельности, таких как строительство, топография, картография, геология и геоинформационные системы. Они позволяют представить сложные географические данные на плоскости с минимальными искажениями.

Топ вопросов за вчера в категории География

География 29.04.2023 13:42 9750 Шамкин Артём

СРОЧНО!!! Сделайте вывод о ресурсообеспеченности стран и регионов мира отдельными видами минеральных

Ответов: 2

География 03.06.2023 18:08 3323 Пономарева Ксюша

Задания 1. Закрасьте разным цветом по пять субъектов Российской Федерации с наиболее высокими (красн

Ответов: 1

География 18.06.2023 05:25 3903 Иванов Сергей

В месторождениях какого региона добывается 90% природного газа страны?​

Ответов: 2

География 26.05.2023 10:20 2902 Лушков Егор

Чем для вас лично интересен 1. Ф. Дрейк 2. В. Баренц 3. А. Тасман 4. Дж. Кук 5. Р. Пири 6. Р. Амундс

Ответов: 2

География 03.06.2023 04:44 3707 Ibragimov Abdrahim

Задания 1. Обозначьте на карте субъект Российской Федерации, в котором вы проживаете, и его центр (с

Ответов: 1

География 17.05.2023 03:48 1745 Голка Кристина

Чем для вас лично интересен Абел Тасман? Помогите пожалуйста

Ответов: 2

География 18.05.2023 02:09 1213 Михайличенко Снежана

Чем для вас лично интересен Виллем Баренц?​

Ответов: 2

География 02.07.2023 16:46 499 Выков Анзор

помогите пожалуйста!! На примере автомобильного завода составьте модель,раскрывающую его связи с дру

Ответов: 2

География 03.06.2023 16:17 1706 Кокорин Илья

Пользуясь данными таблицы, рассчитайте обеспеченность указанных стран и мира нефтью ( т.е чисто лет

Ответов: 1

География 17.05.2023 20:13 1200 Довгополый Виталик

В тексте о химических волокнах выделите абзац. Переведите текстовую информацию в графическую: состав

Ответов: 2

Дирекционный угол

Дирекционный угол (α) – это угол между проходящими через данную точку направлением на ориентир и линией параллельной оси абсцисс, отчитываемой от северного направления оси абсцисс по ходу часовой стрелки оси 0 до 360°.

Дирекционные углы направлений измеряются преимущественно по карте или определяются по магнитным азимутам.

Дирекционный угол ориентирного направления может определяться геодезическим или гироскопическим способом, из астрономических наблюдений, с помощью магнитной стрелки буссоли и по контурным точкам карты (аэрофотоснимка).

При геодезическом способе ориентирования дирекционный угол ориентирного направления может быть получен непосредственно из каталога (списка) координат, решением обратной геодезической задачи по координатам геодезических пунктов, при выполнении засечек или прокладке полигонометрического хода одновременно с определением координат привязываемых точек, а также путем передачи угловым ходом от направления с известным дирекционным углом.

При гироскопическом способе ориентирования с помощью гирокомпаса определяют истинный (астрономический) азимут ориентирного направления, а затем переходят к дирекционному углу этого направления. Азимут ориентирного направления с помощью гирокомпаса определяется по двум, трем (четырем) точкам реверсии. Увеличение числа точек реверсии до трех (четырех) обеспечивает контроль и повышает точность определения дирекционного угла.

При астрономическом способе ориентирования дирекционный угол ориентирного направления определяют путем перехода от азимута светила к азимуту ориентирного направления, а от последнего — к дирекционному углу. Азимут светила вычисляют по результатам наблюдений, выполненных на местности с данной точки. Азимут ориентирного направления из астрономических наблюдений может быть получен и с помощью азимутальной насадки АНБ-1 к буссоли ПАБ-2А непосредственно на местности без выполнения вычислений.

Способ определения дирекционного угла ориентирного направления из астрономических наблюдений является наиболее точным.

Работы в поле при этом способе заключаются в измерении горизонтального угла Q между направлением на светило и заданным направлением в момент времени наведения прибора на светило. По моменту времени наблюдения светила вычисляют азимут а светила, от него переходят к астрономическому азимуту А направления на ориентир: A’ = a + Q. Зная значение сближения меридианов у в точке наблюдения, определяют дирекционный угол с ориентирного направления: a = A — y.

При определении дирекционного угла ориентирного направления с помощью магнитной стрелки буссоли на местности сначала получают магнитный азимут ориентирного направления, а затем, учитывая поправку буссоли, переходят к дирекционному углу. Дирекционный угол ориентирного направления определяется по формуле: а = Ат + (±dАт).

По карте (аэрофотоснимку) дирекционный угол ориентирного направления получают решением обратной геодезической задачи по координатам двух контурных точек Координаты контурных точек при этом определяются по карте (аэрофотоснимку) с помощью циркуля измерителя и поперечного масштаба. Точность полученного дирекционного угла будет тем выше, чем больше расстояние между начальной и ориентирной точками и чем точнее определены координаты этих точек.

Дирекционный угол по карте также можно определить с помощью хордоугломера. Для этого опознают на карте исходную и ориентирную точки, проводят через них прямую линию и получают на карте ориентирное направление. Измерив с помощью хордоугломера угол между северным направлением вертикальной линии километровой сетки карты и ориентирным направлением, получают дирекционный угол этого направления.

Свойства дирекционных углов: дирекционные углы α₁=α₂=α₃ так как параллельные линии пересекаются одной линией. Следовательно, углы равны.

Рисунок 2. — Дирекционные углы.

Дирекционные углы могут быть прямыми и обратными (они отличаются на 180°):

Рисунок 3. — Прямые и обратные дирекционные углы.

В зависимости от выбора системы поверхностных координат или проекции земного эллипсоида на плоскость дирекционный угол может иметь собственное название. Например, геодезическийдирекционный угол, гауссов дирекционный угол и т.д.

Геодезические проекции: основы и принципы

Одним из основных принципов геодезических проекций является сохранение некоторых свойств географических объектов на плоскости карты, таких как форма, углы или расстояния. Это позволяет точно отобразить местоположение объектов в реальном масштабе и соблюдать их пропорции. Однако, невозможно сохранить все свойства одновременно, поэтому различные проекции выбираются в зависимости от конкретных задач и целей картографии.

Геодезические проекции могут быть разделены на классы в зависимости от основного принципа проекции. Например, проекции эквидистантные обеспечивают равенство расстояний на карте, проекции равноугольные сохраняют углы на поверхности Земли, а проекции компромиссные стремятся достичь баланса между равенством расстояний и сохранением углов.

Класс проекции	Описание
Цилиндрические проекции	Образуются проекцией поверхности Земли на образующую цилиндра.
Конические проекции	Образуются проекцией поверхности Земли на образующую конуса.
Плоскостные проекции	Образуются проекцией поверхности Земли на плоскость.

Выбор конкретной геодезической проекции зависит от ряда факторов, таких как размер и форма области, предметы картирования, требования к масштабу и точности, а также методы представления данных. На сегодняшний день существует множество различных геодезических проекций, каждая из которых имеет свои преимущества и ограничения. Правильный выбор проекции играет важную роль в создании точных карт и геодезических измерений.

Системы координат, принятые в геодезии

_______В геодезии применяются следующие системы координат:

• Географическая система координат,
• Зональная система плоских прямоугольных координат Гаусса–Крюгера,
• Полярная система координат.

4.1. Географические координаты

_______С помощью географических координат, то есть широт (φ) и долгот (λ), определяют положение точки относительно экватора и начального меридиана.

_______Широтой (φ) точки называется угол, составленный отвесной линией в данной точке и плоскостью экватора.

_______Долготой (λ) точки называется двугранный угол между плоскостью меридиана данной точки и плоскостью начального меридиана.

https://vk.com/video_ext.php

_______Широта отсчитывается по дуге меридиана к северу и к югу от экватора от 0° до 90°. К северу от экватора широта называется северной, к югу – южной.

_______Долгота отсчитывается от меридиана, проходящего через Гринвич на окраине Лондона. Долгота отсчитывается по дуге экватора или параллели от начального меридиана в сторону востока и запада от 0° до 180°. Долгота к востоку от Гринвичского меридиана называется восточной долготой, к западу – западной. Широты и долготы определяют положение любой точки на земной поверхности и выражаются в угловой мере. Географические координаты определяются из астрономических наблюдений и, а также с помощью геодезических измерений.

4.2. Зональная система плоских прямоугольных координат Гаусса–Крюгера

_______При геодезических работах на больших территориях применяется зональная система плоских прямоугольных координат Гаусса–Крюгера (рис. 4). Для этого земной шар делится меридианами на шестиградусные или трехградусные зоны (рис. 3). Счет зон ведется к востоку от Гринвичского меридиана. Каждая зона проецируется на плоскость таким образом, чтобы средний меридиан зоны был изображен прямой линией. Средний меридиан зоны называется осевым меридианом.

_______Изображение осевого меридиана принимается за ось абсцисс (x), изображение экватора – за ось ординат (y). За начало координат принимают точку пересечения осевого меридиана с экватором.

_______Чтобы не иметь отрицательных ординат, ординату осевого меридиана принимают равной 500 км. Перед ординатой точки указывается номер зоны, в которой точка расположена.