Параметры газа в нормальном состоянии

Изобарный процесс

Изобарный процесс — это изопроцесс, происходящий при постоянном давлении: p = const.

baros — тяжесть, вес.

Закон экспериментально исследовали независимо друг от друга французские физики Жак Шарль (1787) и Жозеф Гей-Люссак (1802).

Работа Ж. Шарля была опубликована уже после открытия Ж. Гей-Люссака. Но изобарный процесс в российских учебниках называют законом Гей-Люссака, в белорусских — законом Шарля.

Закон изобарного процесса: при данной массе газа при постоянном давлении отношение объема к абсолютной температуре есть величина постоянная:

\(~\dfrac{V}{T} = \operatorname{const},\) или \(~\dfrac{V_1}{T_1} = \dfrac{V_2}{T_2} .\)

Этот закон можно записать через температуру t, измеряемую по шкале Цельсия\ где V — объем газа при 0 °С, α = 1/273 К-1 — температурный коэффициент объемного расширения.

Опыт показывает, что при малых плотностях температурный коэффициент объемного расширения не зависит от вида газа, т.е. одинаков для всех газов).

Получить изобарный процесс можно при помощи цилиндра с невесомым поршнем.

Основное уравнение МКТ

Основная задача молекулярно-кинетической теории газа заключается в том, чтобы установить соотношение между давлением газа и его микроскопическими параметрами: массой молекул, их средней скоростью и концентрацией. Это соотношение называется основным уравнением молекулярно-кинетической теории газа или кратко — основным уравнением МКТ.

В основе молекулярно-кинетической теории лежат три положения.

Все вещества образованы из мельчайших частиц — молекул, которые состоят из атомов.

Молекулы химического вещества могут быть простыми и сложными, то есть состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.

Атомы и молекулы находятся в непрерывном хаотическом движении.

Частицы взаимодействуют друг с другом силами, которые имеют электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.

Мы уже выяснили, что причина давления газа на стенки — это удары молекул. Давление напрямую зависит от количества молекул — чем их больше, тем больше ударов о стенки и тем больше давление. А количество молекул в единице объема — это концентрация. Значит, давление газа зависит от концентрации.

Также давление пропорционально квадрату скорости, так как чем больше скорость молекулы, тем чаще она бьется о стенку сосуда. Расчеты показывают, что основное уравнение молекулярно-кинетической теории для идеального газа имеет следующий вид.

Основное уравнение МКТ

p = nkT

p — давление газа

n — концентрация

T — температура газа

m 0 — масса одной молекулы

v — средняя квадратичная скорость [м/с]

Коэффициент 1/3 обусловлен трехмерностью пространства: во время хаотического движения молекул все три направления равноправны.

Важный нюанс: средняя квадратичная скорость сама по себе не в квадрате! Ее формула указана выше, а в основном уравнении МКТ (да и не только в нем) она возведена в квадрат. Это значит, что формулу средней квадратичной скорости нужно подставлять не вместо v 2 , а вместо v — и потом уже возводить эту формулу в квадрат. Это часто провоцирует путаницу.

Мы знаем, что кинетическая энергия вычисляется по следующей формуле:

Кинетическая энергия

Е_к = mv 2 /2

Е_к — кинетическая энергия

m — масса тела

v — скорость [м/с]

Для молекулы газа формула примет вид:

Средняя кинетическая энергия поступательного движения молекулы

Е_к — средняя кинетическая энергия поступательного движения молекулы

m — масса молекулы

v — скорость молекулы [м/с]

Из этой формулы можно выразить mv 2 и подставить в основное уравнение МКТ. Подставим и получим, что давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

Основное уравнение МКТ

p — давление газа

n — концентрация

E — средняя кинетическая энергия поступательного движения молекулы

Дополнительные процессы

На практических занятиях по физике проводятся опыты с адиабатным или адиабатическим процессом (изоэнтропийный), связанным с термодинамикой. В явлении нет теплообмена с внешней средой. Чтобы наблюдать за общим случаем всех вышеописанных процессов, используется газ постоянной теплоёмкостью. Явление называется политропическим.

Если давление и температура составных компонентов одинаково, при этом они взяты в равных объёмах, тогда в используемых идеальных газах содержится одно число молекул. На долю одного моля разных веществ приходится N A =6,02·10 23молекул. Это считается числом Авогадро.

По закону Дальтона, давление смеси равно сумме парциальных P, входящих в состав. Выражение записывается следующим образом: P cm=P1+P2+…Pn. Последний показатель Pn является давлением газа, который бы занимал весь объёмом сосуда.

Чаще в старших классах физике рассматриваются изохорические процессы, когда переходит идеальный газ из одного состояния в другое, при этом не изменяется его объёмом. Явление впервые рассмотрел француз Жак Шарль. Закон записывается следующим образом: PV=vRT. Так как v= const и V=const, поэтому для любых разных состояний веществ используется равенство: P1/T1=P2/T2=….Pn/Tn. Закон Шарля математически записывается так: P/T=const.

Из выражения следует, что между температурой и давлением наблюдается прямо пропорциональная связь. Если увеличивается P, тогда повышается T, и наоборот. График зависимости данных величин называется изохорой. На промежутке абсолютного нуля для кривых предусмотрена условная зависимость. Прямая доводится до начала координат с помощью пунктирных линий.

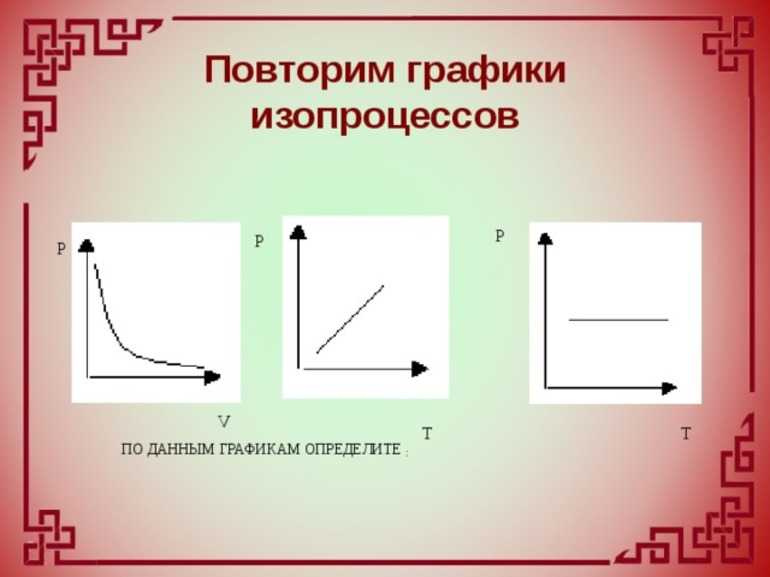
Подобная зависимость T от P и V при изобарных и изохорных процессах определяет точность и эффективность измерения температуры газовыми термометрами. Первыми ученые открыли эти явления, которые считаются частными случаями уравнения состояния. Позже физики утвердили закон Клапейрона и Менделеева.

Если следовать хронологии, сначала изучались процессы, которые протекали при постоянной температуре, а затем при одном объеме. Последними рассматривались изобарические процессы. Редким и интересным явлением считается изоэнтропия, когда изменяется термодинамическая система при условии постоянной энтропии. Последнее записывается как S=const.

Хранение и транспортировка газов

Если нужно перевезти значительное количество газа из одного места в другое или если газ необходимо длительно хранить, его помещают в специальные прочные металлические сосуды. Из-за того, что при уменьшении объема увеличивается давление, газ можно закачать в небольшой баллон, но он должен быть очень прочным.

Сосуды, предназначенные для транспортировки газов, выдерживают высокие давления. Поэтому с помощью специальных насосов (компрессоров) туда можно закачать значительные массы газа, которые в обычных условиях занимали бы в сотни раз больший объем.

Поскольку давление газов в баллонах даже при комнатной температуре очень велико, их ни в коем случае нельзя нагревать. Например, держать под прямыми лучами солнца или пытаться сделать в них отверстие — даже после использования.

• Хронологическая таблица крылова кратко

    

• Где добывают полезные ископаемые осадочного происхождения в россии кратко

    

• Исторические разновидности понимания истины кратко

    

• Климат венеры планеты кратко

    

• Судебная экспертиза кратко учебник

Зависимость давления от других величин

Зависимость давления от объема

В механике есть формула давления, которая показывает, что давление прямо пропорционально силе и обратно пропорционально площади, на которую эта сила оказывается.

Давление

p = F/S

F — сила

S — площадь

То есть если наши двести миллионов комаров будут толкать легковую машину, они распределятся по меньшей площади, чем если бы толкали грузовой автомобиль, — просто потому, что легковушка меньше грузовика. Из формулы давления следует, что давление на легковой автомобиль будет больше из-за его меньшей площади.

Рассмотрим аналогичный пример с двумя сосудами разной площади.

Давление в левом сосуде будет больше, чем во втором, потому что его площадь меньше. А раз меньше площадь сосуда, то меньше и его объем. Значит, давление зависит от объема следующим образом: чем больше объем, тем меньше давление, и наоборот.

При этом зависимость будет не линейная, а примет вот такой вид (при условии, что температура постоянна):

Зависимость давления от объема называется законом Бойля-Мариотта. Она экспериментально проверяется с помощью такой установки:

Объем шприца увеличивают с помощью насоса, а манометр измеряет давление. Эксперимент показывает, что при увеличении объема давление действительно уменьшается.

Зависимость давления от температуры

Рассмотрим зависимость давления газа от температуры при условии неизменного объема определенной массы газа. Исследования в этой области впервые провел французский изобретатель Жак Шарль в XVIII веке.

В ходе эксперимента газ нагревали в большой колбе, соединенной с ртутным манометром в виде узкой изогнутой трубки. Незначительным увеличением объема колбы при нагревании можно пренебречь, как и столь же незначительным изменением объема при смещении ртути в узкой манометрической трубке. Таким образом, объем газа можно считать неизменным.

Подогревая воду в сосуде, окружающем колбу, ученый измерял температуру газа термометром, а давление — манометром.

Эксперимент показал, что давление газа увеличивается с увеличением температуры. Это связано с тем, что при нагревании молекулы газа движутся быстрее, из-за чего чаще ударяются о стенки сосуда.

С температурой все проще. Зависимость давления от температуры при постоянных объеме и массе будет линейной:

Эта зависимость называется законом Шарля в честь ученого, открывшего ее.

Что такое давление

Давлением $(p)\ $называют физическую величину, равную:

где $F_n$ — проекция силы на нормаль к участку тела $\triangle S$, $\triangle S$- площадь тела. Давление газа создается в результате многочисленных ударов молекул о стенки сосуда, в котором он находится. Очевидно, что давление зависит от скорости движения молекул газа, их массы и количества.

Единица измерения давления в системе СИ паскаль — $\frac$=Па. К альтернативным единицам измерения давления относят — техническую атмосферу, которая равна $1 атм=1 кгс/см^2$. Также для измерения давления применяют высоту столба жидкости (воды, ртути, спирта) в капилляре, если давление небольшое. При этом давление рассчитывается по формуле:

\

где $\rho $- плотность вещества (жидкости) в $кг/м^3$, $g=9,80665(м/c^2)$- ускорение свободного падения, соответственно:

В таком случае считают, что давление измеряется в м вод. ст. (метр водяного столба) или мм.рт.ст (миллиметр ртутного столба).

Давление иногда разделяют на: атмосферное, избыточное и давление в вакууме (т.е. ниже атмосферного).

Удельным объемом $V_u$ называют величину, обратную плотности $\rho :\ $

Для однородного тела удельный объем:

В системе СИ за единицу количества вещества принят моль. Количество одинаковых частиц, содержащихся в одном моле, называют постоянной (числом) Авогадро $N_A=6,022\cdot ^ моль^$.

Модель идеального газа

В физике есть такое понятие, как модель. Модель — это что-то идеализированное, она нужна в случаях, когда можно пренебречь некоторыми параметрами объекта или процесса.

Идеальный газ — это модель реального газа. Молекулы идеального газа представляют собой материальные точки, которые не взаимодействуют друг с другом на расстоянии, но взаимодействуют при столкновениях друг с другом или со стенками сосуда. При работе с идеальным газом можно пренебречь потенциальной энергией молекул (но не кинетической).

Модель идеального газа не может описать ситуацию, когда газ сжимают так сильно, что он конденсируется — переходит в жидкое состояние.

В повседневной жизни идеальный газ, конечно, не встречается. Но реальный газ может вести себя почти как идеальный. Такое случается, если среднее расстояние между молекулами во много раз больше их размеров, то есть если газ очень разреженный.

§ 5. Уравнение состояния идеального газа

Выясним, как связаны между собой макроскопические параметры идеального газа, которые характеризуют его равновесное состояние: давление, масса всего газа, объём, предоставленный ему, и температура.

Состояние макроскопической системы полностью определено, если известны её макроскопические параметры — давление , масса , температура  и объём . Уравнение, связывающее параметры данного состояния, называют уравнением состояния системы. Изменение параметров состояния системы с течением времени называют процессом.

Если при переходе идеального газа из одного состояния в другое число его молекул  остаётся постоянным, т. е. масса и молярная масса газа не изменяются, то из уравнений  и  следует:

,  ,

(5.1)

где  — постоянная Больцмана;  — параметры начального состояния газа, а  — конечного. Из соотношений (5.1) следует, что

,

или

. 

(5.2)

При неизменных массе и молярной массе идеального газа отношение произведения его давления и объёма к абсолютной температуре является величиной постоянной.

Уравнение (5.2) связывает два рассматриваемых состояния идеального газа независимо от того, каким образом газ перешёл из одного состояния в другое.

Уравнение состояния в виде (5.2) впервые вывел в 1834 г. французский физик Бенуа Клапейрон (1799–1864), поэтому его называют уравнением Клапейрона.

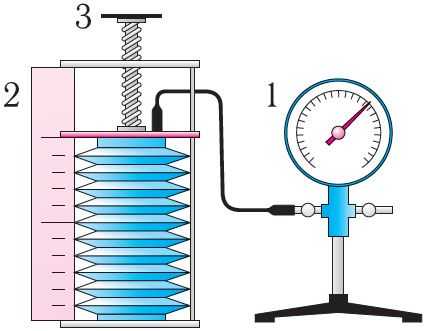Рис. 18

В справедливости уравнения состояния можно убедиться, воспользовавшись установкой, изображённой на рисунке 18. Манометром 1, соединённым с герметичным гофрированным сосудом, регистрируют давление газа внутри сосуда. Объём газа в сосуде можно рассчитать, используя линейку 2. Температура газа в сосуде равна температуре окружающей среды и может быть измерена термометром.

Измерив параметры газа  в начальном состоянии, вычисляют отношение . Затем помещают сосуд в горячую воду. При этом температура газа и его давление изменяются. Вращая винт 3, изменяют вместимость сосуда. Измерив снова давление газа  и температуру , а также рассчитав предоставленный ему объём , вычисляют отношение  Как показывают расчёты, уравнение состояния (5.2) выполняется в пределах погрешности эксперимента.

Уравнение состояния (5.2) можно применять для газов при следующих условиях:

1) не очень большие давления (пока собственный объём всех молекул газа пренебрежимо мал по сравнению с предоставленным ему объёмом);

2) не слишком низкие или же высокие температуры (пока абсолютное значение потенциальной энергии межмолекулярного взаимодействия пренебрежимо мало по сравнению с кинетической энергией теплового движения молекул).

От теории к практике

Рис. 19

На рисунке 19 представлен график процесса перехода идеального газа данной массы из состояния 1 в состояние 2. Как изменился объём газа в результате этого процесса?

Поскольку число частиц , то из уравнения (5.1) следует:

.

(5.3)

Величину, равную произведению постоянной Больцмана  и постоянной Авогадро , назвали универсальной газовой постоянной :

.

(5.4)

С учётом выражения (5.4) уравнение (5.3) примет вид:

. 

(5.5)

Поскольку количество вещества , то формулу (5.5) можно записать в виде:

.

Уравнение состояния в виде (5.5) впервые получил русский учёный Д. И. Менделеев (1834–1907) в 1874 г., поэтому его называют уравнением Клапейрона–Менделеева.

Отметим, что уравнение Клапейрона–Менделеева связывает между собой макроскопические параметры конкретного состояния идеального газа. Используя уравнение Клапейрона–Менделеева, можно описать различные процессы, происходящие в идеальном газе.

Газ: агрегатное состояние

У веществ есть три агрегатных состояния — твердое, жидкое и газообразное.

Их характеристики — в таблице:

Агрегатные состояния

Свойства

Расположение молекул

Расстояние между молекулами

Движение молекулы

Твердое

сохраняет форму и объем

в кристаллической решетке

соотносится с размером молекул

колеблется около положения равновесия в кристаллической решетке

Жидкое

сохраняет объем и текучесть

близко друг к другу

молекулы малоподвижны, при нагревании скорость движения увеличивается

Газообразное

занимает весь предоставленный объем

больше размеров молекул

хаотичное и непрерывное

В жизни мы встречаем вещества в газообразном состоянии, когда чувствуем запахи. Запах очень легко распространяется, потому что газ не имеет ни формы, ни объема (занимает весь предоставленный объем) и состоит из хаотично движущихся молекул, расстояние между которыми больше, чем размеры молекул.

Агрегатных состояний точно три?

На самом деле есть еще четвертое — плазма. Звучит как что-то из научной фантастики, но это просто ионизированный газ — газ, в котором, помимо нейтральных частиц, есть еще и заряженные. Ионизаторы воздуха как раз строятся на принципе перехода из газообразного вещества в плазму.

Законы Авогадро и Дальтона

Из уравнения состояния вытекают два следствия:

1. Из формулы (1) получим \(~N = \dfrac{p \cdot V}{k \cdot T}\), откуда видно, что если различные газы занимают при одинаковых температурах и одинаковых давлениях равные объемы, то число N молекул у них тоже одинаково, т.е. вытекает установленный опытным путем закон Авогадро: при равных давлениях и температурах в одинаковых объемах любых газов содержится одинаковое число молекул.
2. Пусть в сосуде имеется смесь газов, каждый из которых при отсутствии других оказывает соответственно давление p₁, p₂, … (парциальные давления газов). Запишем для каждого газа уравнение состояния:
   \(~p_1 \cdot V = N_1 \cdot k\cdot T, p_2 \cdot V = N_2 \cdot k \cdot T, \ldots\)
   

   и сложим их:

   
   \(~p_1+ p_2 + \ldots = \dfrac{(N_1+ N_2 + \ldots) \cdot k \cdot T}{V} = \dfrac{N \cdot k \cdot T}{V},\)
   

   где N₁ + N₂ + … = N — число молекул смеси газов. Но \(~\dfrac{N \cdot k \cdot T}{V} = p\) .
   Следовательно, p = p₁ + p₂ + …, т.е давление смеси газов равно сумме парциальных давлений каждого из газов — это закон Дальтона, открытый им в 1801 г. экспериментально.