Формулировка обобщенной теоремы фалеса

Содержание

Слайд 1
Четырехугольники
8классгеометрия

Урок№ 4
Трапеция
04.12.2012
1
www.konspekturoka.ru
Ввести понятие трапеции и ее элементов.
Познакомить с равнобедренной и прямоугольной трапецией.
Рассмотреть свойства равнобедренной трапеции.

Слайд 2
04.12.2012
www.konspekturoka.ru
2
А
В
С
D
Трапецией называется
четырехугольник, у которого две стороны параллельны,адве другие непараллельны.
Основание
Основание
Боковая
Боковая
АВСD – трапеция, если ВС∥AD,
АВ и СD – боковые стороны,
ВС и AD – основания.

Слайд 3
04.12.2012
www.konspekturoka.ru
3
Трапецияназывается равнобедренной,
если ее боковые стороны равны.

А
В
С
D
АВСD – равнобедренная трапеция,если ВС∥ AD,
АВ = СD – боковые стороны.

Слайд 4
04.12.2012
www.konspekturoka.ru
4
А
В
С
D
Трапецияназывается прямоугольной,
если один из углов прямой.

АВСD – прямоугольная трапеция, если ВС∥ AD,
∠А = 90° или ∠В= 90°.

Слайд 5
04.12.2012
www.konspekturoka.ru
5
А
В
С
D
М
N
М – середина АВ
N – середина CD
MN – средняя линия трапеции

Слайд 6
04.12.2012
www.konspekturoka.ru
6

А
В
С
D
ВD= AC – диагонали трапеции

∠А = ∠D, ∠В = ∠С – углы при основаниях
Свойства равнобедренной трапеции
2. В равнобедренной трапеции углы при каждом основании равны.
1. В равнобедренной трапеции диагонали равны.

Слайд 7
04.12.2012
www.konspekturoka.ru
7

А
В
С
D
ВD= AC – диагонали трапеции

∠А = ∠D, ∠В = ∠С – углы при основаниях
Признаки равнобедренной трапеции
2. Если углы при основании трапеции равны, то она равнобедренная.
1. Если диагонали трапеции равны, то она равнобедренная.

Слайд 8
04.12.2012
www.konspekturoka.ru
8
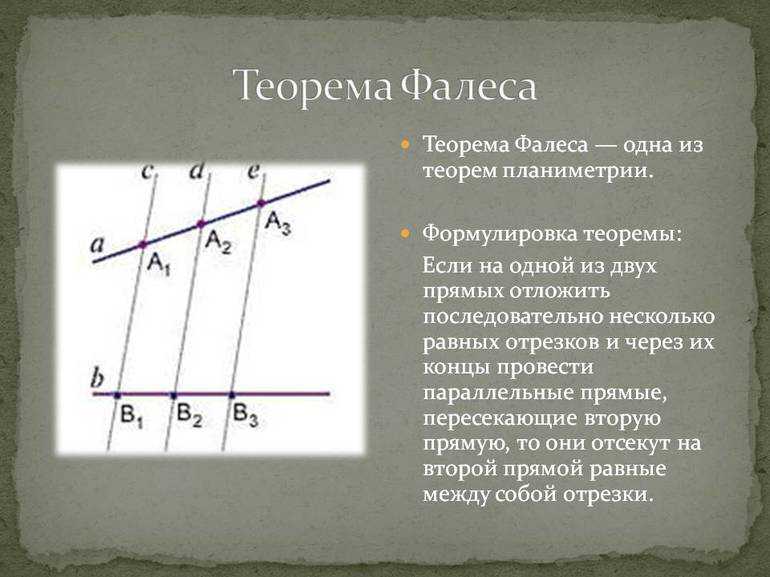
Теорема Фалеса
Если на одной из двух прямых отложить последовательно
равных несколько отрезков и через их концы провести
параллельные прямые, пересекающие вторую прямую,
то они отсекут на второй прямой равные между собой
отрезки.
а) l₁ ∥ l₂
б) l₁ ∥ l₂
А₁
А₂
А₃
А₄
А₅
В₁
В₂
В₃
В₄
В₅
А₁А₂ = В₁В₂
l₁
l₁
l₂
l₂
А₁
А₂
А₃
А₄
А₅
А₁А₂ В₂ В₁ — параллелограмм
В₁
В₂
В₃
В₄
В₅
l
С
D
l₁ ∥ l
А₂ А₃DC — параллелограмм
А₂A₃ = CD
А₂A₃ = В₂B₃

Слайд 9
04.12.2012
www.konspekturoka.ru
9
Задача
1
Доказательство
Докажите, что отрезок, соединяющий середины боковых
сторон трапеции, параллелен основаниям трапеции.
А
В
С
D
Пусть Е – середина АВ.
Проведем ЕF ∥ BC ∥ AD.
.
F
.
E
Точка F – середина CD
(по теореме Фалеса).
Докажем, что ЕF — единственный
Через точки Е и F можно провести только одну прямую
(аксиома) т. е. отрезок, соединяющий середины боковых
сторон трапеции ABCD параллелен основаниям, ч. т

д.

Слайд 10
04.12.2012
www.konspekturoka.ru
10
Задача
2
Дано:
Найти:
А
В
С
D
АВСD – трапеция, ∠A = 36°, ∠C = 117°
∠В = ?, ∠D = ?
36°
117°
Решение
АВСD – трапеция, то ВС∥ AD.
∠А + ∠В = 180°
36° + ∠В = 180°
∠В = 180° — 36°
∠В = 144°
∠С + ∠D = 180°
∠117° + ∠D = 180°
∠D = 180° — ∠117°
∠D = 63°
Ответ:
∠В = 144°,
∠D = 63°

Слайд 11
04.12.2012
www.konspekturoka.ru
11
Задача
3
Дано:
Найти:
АВСD – равнобокая трапеция, ∠A = 68°,
∠В = ?, ∠С -?, ∠D = ?
Решение
Если АВСD – равнобокая трапеция,
то ∠A = ∠D = 68°,

А
В
С
D
68°
68°
∠ 68°+ ∠В = 180°
∠В = 180° — ∠ 68°
∠В = 112°
∠В = ∠С = 112°,
Ответ:
∠D = 68°,
∠В = 112°,
∠С = 112°.

Слайд 12
∟
В₁
04.12.2012
www.konspekturoka.ru
12
Задача
4
Дано:
Найти:
АВСD – прямоугольная трапеция,
∠D = 90°, BC = 4 см, AD = 7 см, ∠A = 60°

АВ — ?
Решение
Проведем ВВ₁ ⊥ AD
4 см
7 см
60°
AВ₁ = AD — B₁D

А
В
С
D
AВ₁ = 7 — 4 = 3 (см)
Рассмотрим ∆ АBВ₁:

∠A = 60° — по условию,
∠В₁ = 90° так как ВВ₁ ⊥ AD, то ∠В = 30°
AВ₁ = ½АВ – по свойству прямоугольного треугольника,
АВ= 3· 2 = 6 (см).
Ответ:
6 (см).

Слайд 13
04.12.2012
13
Ответить на вопросы:
www.konspekturoka.ru
Спасибо за внимание!
Какой четырехугольник называется трапецией?
Как называются стороны трапеции?
Какая трапеция называется прямоугольной? Равнобедренной?
Сформулируйте свойства равнобедренной трапеции. Сформулируйте признаки равнобедренной трапеции.
Что такое средняя линия трапеции? Свойство средней
линии трапеции.

Посмотреть все слайды

Теорема Фалеса.

Если стороны
угла пересечены параллельными прямыми, то отрезки, отсекаемые ими на одной
стороне этого угла, пропорциональны соответственным отрезкам, отсекаемым
ими на другой его стороне.

Обратная теорема Фалеса.

Если на одной
стороне угла от его вершины O отложены
отрезки OA, AB, BC, … и
на другой его стороне также от вершины O
отложены соответственно пропорциональные им отрезки OA₁, A₁B₁, B₁C₁,
… (OA/OA₁= AB/AB₂= BC/BC₂=k), то прямые
AA₁, BB₁, CC₁,
— параллельны.

Тренировочная работа №10 задание 16.

Точки В₁ и С₁ лежат на сторонах
соответственно AC и AB треугольника ABC, причем АВ₁: В₁С
= АС₁: С₁В. Прямые ВВ₁ и СС₁ пересекаются
в точке О.

а) Докажите, что прямая АО делит пополам сторону BC.

б) Найдите отношение площади четырехугольника АВ₁ОС₁
к площади треугольника ABC, если известно, что АВ₁: В₁С =
АС₁: С₁В = 1:4.

Решение:

а) Так как точки В₁ и С₁ делят
стороны треугольника в одинаковых отношениях, то по теореме обратной теореме
Фалеса прямая В₁С₁ всегда будет параллельна BC. Отсюда
следует, что четырёхугольник ВСВ₁С₁
– трапеция. По теореме о четырех точках трапеции середины оснований, точка
пересечения диагоналей и точка пересечения боковых сторон лежат на одной
прямой. Таким образом, прямая АО проходит через середины оснований трапеции ВСВ₁С₁.

б) Треугольник АВ₁С₁ подобен
треугольнику АВС с коэффициентом подобия 1/5, следовательно, его площадь будет
составлять 1/25 площади треугольника АВС или S/25. Тогда площадь трапеции ВСВ₁С₁ составляет
24/25 площади треугольника АВС, то есть 24S/25.  
Высота треугольника ВВ₁С₁, проведённая к стороне В₁С₁,
равна высоте треугольника ВВ₁С, проведённой к стороне ВС. Поскольку В₁С₁в
пять раз меньше ВС, то площадь треугольника ВВ₁С₁в пять
раз меньше, чем площадь треугольника ВВ₁С₁. Обозначим площадь
треугольника ВВ₁С₁ – х,
тогда площадь треугольника ВВ₁С – 5х. 

Значит, х + 5х =
24S/25,  6х = 24S/25, х = 4S/25. То есть

площадь треугольника ВВ₁С₁ равна
4S/25,

площадь треугольника ВВ₁С равна 20S/25.

Рассмотрим треугольники ВСС₁ и ВСВ₁.
Так как у них общее основание – ВС, и одинаковая высота, то их площади равны. В
состав каждого из них входит треугольник ОВС, поэтому площади треугольников ВВ₁С₁
и СВ₁С₁ равны, пусть они равны р.

Треугольники ОВ₁С₁ и ОВС подобны
с коэффициентом подобия 1/5. Если обозначим площадь треугольника ОВ₁С₁
через а, то площадь
треугольника ОВСравна 25а.

Так как площадь треугольника ВВ₁С₁
равна сумме площадей треугольников ВОСи В₁ОС, получаем 4S/25 = а +р.

Так как площадь треугольника ВВ₁С равна
сумме площадей треугольников ОВ₁С₁ и ВОС₁,
получаем 20S/25 =25 а +р. Вычитая из
этого равенства предыдущее, получаем

16S/25 =24а.Отсюда а = 2S/75.

Площадь четырехугольника АВ₁ОС₁ =
S/25 +2S/75 = S/15

Основные понятия

Фалесом было доказано, что две прямые линии RF и NS называются параллельными исключительно в том случае, если они проложены в одной плоскости и не пересекаются между собой вне зависимости от длины. Это правило всегда обозначают как RF || NS.

Абсолютно все существующие точки конкретной прямой располагаются на неизменном расстоянии от второй линии. А это значит, что все линии, которые параллельны одной прямой, являются параллельными между собой. Математики полагают, что итоговый угол между параллельными линиями приравнивается 0. Но это утверждение актуально только в том случае, если у отрезков одинаковые направления и они расположены под углом 180 градусов.

В качестве наглядного примера можно рассмотреть ситуацию, когда перпендикуляры RF, NS, EF относятся к одной и той же прямой РЕ и параллельны между собой. При этом прямая РЕ перпендикулярна ко всем остальным линиям. Итоговая длина сформированного отрезка перпендикуляра, расположенного между двумя параллельными прямыми, соответствует расстоянию средних линий. При изучении пространственной теоремы обязательно нужно понимать, что сразу восемь углов возникает при пересечении двух параллельных прямых третьей прямойю

Представленная специалистами формулировка теоремы Фалеса содержит много нюансов, в которых обязательно должен разбираться каждый человек, планирующий решать различные математические задачи. В противном случае будет сложно избежать самых распространённых ошибок. Даже кратко изложенная теория позволяет разобраться в главных математических тонкостях. Чтобы ученику стало понятно то, как именно нужно использовать теорему, можно задействовать специальные таблицы, которые помогут расширить итоговые математические возможности.

Огромные заслуги талантливого математика

В своё время Фалес Милетский был главным основателем Ионийской школы. Неоценимой заслугой этого человека было создание многофункциональной научной геометрии. Великий учёный специфического египетского искусства измерения смог самостоятельно создать полезную для человечества дедуктивную геометрию.

Благодаря целеустремлённости Фалеса все доступные в то время знания были оперативно переведены в научную категорию. Математик смог донести результаты своих наблюдений до того уровня, который подходит для учеников школ, указав при этом на определённый комплекс понятий. Доказанная талантливым и наблюдательным Фалесом теорема играет одну из самых важных ролей в геометрии. Она была хорошо известна не только в Древнем Египте, но и в других крупных странах. Актуальность и многогранность теоремы позволяет специалистам ежедневно строить новые здания, дороги и другие конструкции.

Фалес смог при помощи обычного посоха и тени установить габариты египетской пирамиды. Для этого он в обычный ясный день закрепил свой массивный посох на том участке, на котором заканчивалась тень от величественного сооружения. Он весь день прождал того момента, когда итоговая длина имеющейся тени от посоха максимально сравнялась с его высотой, после он измерил длину тени.

Историческая справка

Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между отрезками. Очень часто при этом приходится проводить дополнительный отрезок.

Аргентинская музыкальная группа представила песню, посвящённую теореме. В видеоклипе для этой песни приводится доказательство для прямой теоремы для пропорциональных отрезков.

Видео:Обратная теорема Фалеса #математика #егэ2023 #математикапрофиль2023 #fypСкачать

Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга.

Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.

Топ вопросов за вчера в категории Геометрия

Геометрия 09.04.2020 09:49 2341 Тулегалиев Аслан

Две стороны треугольника равны 10 см и 12 см, а угол между ними 120 градусов. Нужно найти третью сто

Ответов: 1

Геометрия 04.06.2023 15:41 889 Жебрикова Ирина

На рисунке изображён план сельской местности. Оля на летних каникулах приезжает в гости к дедушке в

Ответов: 1

Геометрия 19.06.2023 21:31 1116 Смирнов Евгений

Четырёхугольник SPQR описан возле окружности, PQ = 19, QR = 24, RS = 20найди SP​

Ответов: 1

Геометрия 28.02.2021 04:29 1267 Шишов Вова

Найдите радиус окружности описанной около треугольника со сторонами 13,20,21​

Ответов: 2

Геометрия 20.06.2023 03:05 2709 Овсянников Никита

На диагонали BD параллелограмма ABCD отметили точки M и K так, что ∠BAM = ∠DCK (точка M лежит между

Ответов: 2

Геометрия 20.06.2023 03:05 3349 Саргсян Мариам

Один из углов ромба равен 64°. Найдите углы, которые образует сторона ромба с его диагоналями. Обяза

Ответов: 1

Геометрия 04.06.2023 23:48 1706 Бабич Илья

Точки M и N принадлежат соответственно граням SBC и SAC пирамиды SABC. Постройте точку пересечения п

Ответов: 1

Геометрия 16.05.2023 17:08 1105 Сысойкин Евгений

На рисунке OA = OD, OB=OC, угол ACO=75, угол ABO=20, Найди угол ACD

Ответов: 2

Геометрия 19.06.2023 06:23 1080 Тулекбаев Айдос

Дан ромб MNKL. Угол KML относится к углу NLM, как 3 к 7. Определи значения углов ромба. Запиши отв

Ответов: 1

Геометрия 12.06.2023 04:48 421 Малахов Никита

На рисунке OA = OD, OB=OC, угол ACO=60, угол ABO=25, Найди угол ACD

Ответов: 2

Основные понятия

Прежде чем сформулировать и доказать теорему Фалеса, напомним некоторые важные определения геометрии:

• квадрат;
• параллелограмм;
• трапеция.

У квадрата четыре угла.

Параллелограмм – это квадрат, противоположные стороны которого попарно параллельны друг другу. В параллелограмме противоположные стороны и противоположные углы равны.

Трапеция – это квадрат, у которого две противоположные стороны параллельны друг другу, а две другие противоположные стороны не параллельны друг другу.

Для понимания приведем примеры задач с параллелограммом и трапецией.

Пример 1

Задача. Найдите углы параллелограмма ABCD, если angle A=73^{circ}.

Решение. Давайте создадим этот рисунок:

Рисунок 1. Параллелограмм. Author24 — онлайн-биржа студенческих работ

На рисунке проведена прямая, параллельная AB, из вершины B. Угол, образованный вершиной B, проведенной прямой, и стороной BC, равен 73^{circ}, лежащей поперек угла A. По определению прямого угла (прямой угол равен 180^{circ}) получаем простые вычисления:

угол B=180-73=107^{circ}. Так как в параллелограмме противоположные углы равны, то angle C=angle A=73^{circ}, angle D=angle B=107^{circ}.

Отвечать. 73 ^ { circ}, 73 ^ { circ}, 107 ^ { circ}, 107 ^ { circ}.

В приведенном выше примере с помощью свойства четырехугольников удалось решить, что сумма углов выпуклого четырехугольника равна $360^{circle}$. Для этого нужно было бы дополнительно доказать, что параллелограмм является выпуклым четырехугольником. Этот простой вопрос предоставляется читателю для размышления на досуге.

Пример 2

Задача. Найдите угол B и угол D в трапеции ABCD, если угол A = 47^{circle}, angle C = 108^{circle}.

Решение. Сделаем рисунок:

Рисунок 2. Трапеция. Author24 — онлайн-биржа студенческих работ

На рисунке проведена прямая, параллельная AB, из вершины B. Угол, образованный вершиной B, проведенной прямой и стороной BC, равен 47^{circ}, лежащему поперек угла A. По определению прямого угла получаем простые вычисления: angle B=180-47=133^{circ}.

На рисунке также проведена линия, параллельная CD, из вершины D. Угол, образованный вершиной D, проведенной прямой и стороной CD, равен 108^{circ}, лежащей выше угла C. По определению прямого угла получаем простые вычисления: angle B=180-108=72^{circ}.

Отвечать. 133 ^ { circ}, 72 ^ { circ}.

Как и в случае с параллелограммом, эту задачу можно проверить, сложив вместе все углы данной трапеции. Их сумма должна быть равна 360^{circ}. Видно, что сумма всех углов этой трапеции на самом деле равна 360.

Освоив ключевые понятия, мы можем перейти к теореме Фалеса и ее доказательству.

Вариации и обобщения

Видео:Геометрия 8 класс : Теорема ФалесаСкачать

Используемая в геометрии теорема Фалеса с доказательством имеет много нюансов, которые нужно учитывать тем, кто решил изучить эту тему. Если абсолютно идентичные отрезки начинаются от вершины треугольника, то и обратная форма теоремы будет уместной. Для пересекающихся линий предназначена следующая формулировка: если 2 линии пересекают ближайшие прямые, отсекая при этом равные между собой отрезки начиная от самой верхней части, то такие прямые считаются параллельными. Эти нюансы часто не учитывают учащиеся, из-за чего допускают грубые ошибки.

Максимального сходства отрезков на обеих секущих линиях нужно требовать в том случае, если секущие являются параллельными. В противном случае утверждение становится неактуальным. Учащимся нелишним будет узнать следующий закон: L является математическим соответствием между двумя точками прямых линий w и q. Тогда элементарное множество прямых D L (D) будет множеством касательных к некоторому коническому сечению. В приведённой Фалесом теореме в роли конического сечения будет выступать удалённая точка, которая максимально соответствует направлению параллельных линий.

Ключевые особенности теоремы

Когда учащийся попробует на одной из двух прямых линий отложить разные отрезки, а потом через их концы провести параллельные линии, которые будут пересекать вторую прямую, то в итоге на второй прямой они обязательно отсекут идентичные между собой отрезки. Даже в школьной математике часто пользуются обобщённой теоремой Фалеса: те отрезки, которые формируются только благодаря параллельным прямым на одной линии, являются пропорциональными по отношению к другой прямой линии.

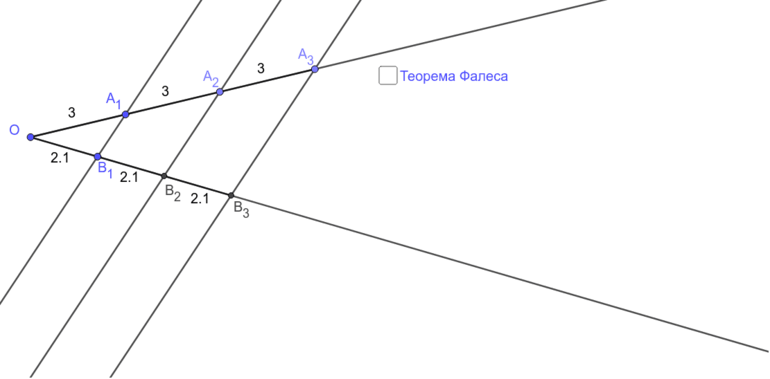
Наглядное доказательство

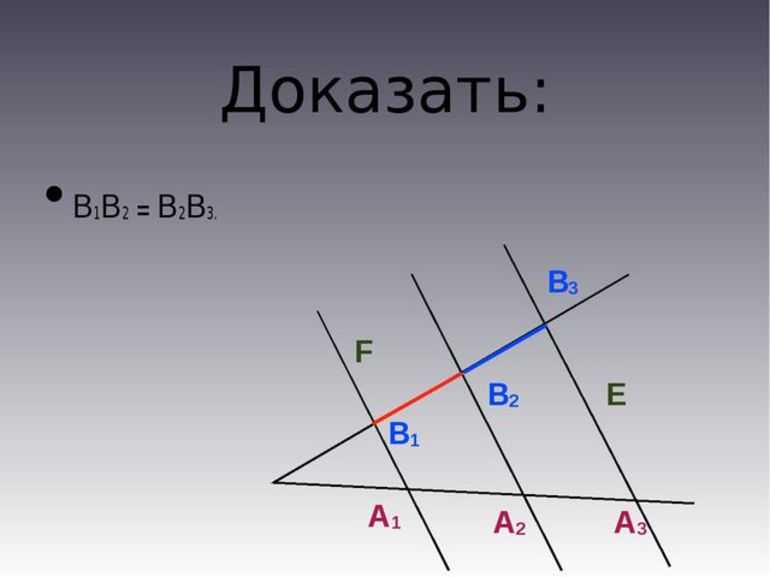
В качестве примера можно взять точки Н1, Н2 и Н3, которые служат для обозначения пересечения используемых параллельных отрезков только с одной стороны угла. А вот для обозначения точек пересечения этих прямых с другой стороны угла используется К1, К2 и К3. Если через точку К2 провести небольшую прямую Т1 и Т2, а также параллельную Н1 и Н2, то в итоге получится обычный параллелограмм: Н1Т1КН2 и Н2К2Т2Н3. Из этого результата можно понять, что Н1Н2 = Т1К2 и Н2Н3 = К2Т2. Этот результат был достигнут благодаря тому, что Н1Н2 = Н2Н3, а Т1К1 = К2Т2.

? Т1В2В1 = ? Т2В2В3 — это утверждение актуально только по отношению ко второму признаку равенства треугольников. Можно понять, что Т1В2 = В2Т2, < Т1В2В1 = < Т2В2В3 (как вертикальные треугольники). < В1Т1В2 = < = В3Т2В2 (как внутренние накрест лежащие треугольники при прямых линиях В1Т1 и Т2В3, а также секущем отрезке Т1Т2). Из установленного равенства треугольников получается, что В1В2 = В2В3. На этом можно считать, что теорема в геометрии полностью доказана. Если всё сделано правильно, то в итоге должна получиться следующая формула: (АВ = ВТ, АА1 || ВВ1 ||ТТ1) А1В1 = В1Т1.

Интересные нюансы из истории

Обобщение теоремы позволило современным математикам понять пропорциональность конкретного отрезка. Действующее правило гласит, что параллельные прямые, которые пересекают стороны угла, отсекают пропорциональные отрезки. Формула выглядит следующим образом: АА1 || ВВ1 || ТТ1 → АВ ВС = А1В1/В1Т1.

Применение обобщённой теоремы имеет несколько интересных исторических фактов:

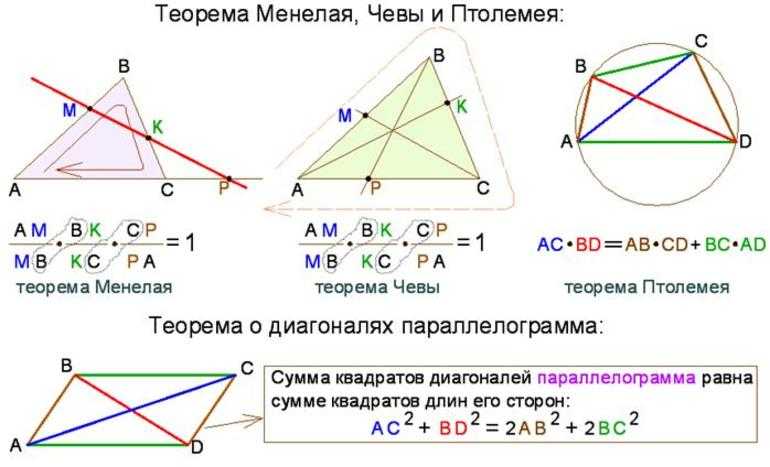
1. За пределами русской литературы широко распространённой теоремой известного математика Фалеса принято называть раздел евклидовой геометрии. Утверждение касается того, что сформированный угол, который базируется на определённом диаметре окружности, является прямым. Доказательство этой удивительной теоремы действительно приписывают Фалесу, так как этому есть письменное доказательство, которое удалось сберечь.
2. Теоремы Менелая, Фалеса и Чевы используются в первую очередь тогда, когда в условиях задачи были даны соотношения между отрезками. Чаще всего для поиска правильного решения приходится проводить вспомогательный отрезок.
3. В морской отрасли активно используется теорема при построении навигации. Она применяется в качества основного правила о том, что столкновение кораблей, которые движутся по волнам с одинаковой скоростью, неизбежно, если сохранится ранее заданный курс движения.
4. Известная в Аргентине группа представила песню, которая посвящена теореме. В представленном клипе для этой песни было приведено доказательство для прямой теоремы используемых пропорциональных отрезков.
5. Все азы геометрии Фалес постигал на территории Древнего Египта.

Свойство средней линии трапеции

Средней линией трапеции называют отрезок, соединяющий середины ее боковых сторон.

Рассмотрим свойство средней линии трапеции.

Теорема (свойство средней линии трапеции). Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство:

Пусть — данная трапеция, — ее средняя линия (рис. 109). Докажем, что   и

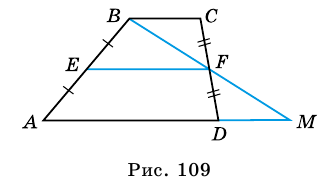
1) Проведем луч до его пересечения с лучом Пусть — точка их пересечения. Тогда (как внутренние накрест лежащие при параллельных прямых  и и секущей (как вертикальные), (по условию). Следовательно, (по стороне и двум прилежащим углам), откуда   (как соответственные стороны равных треугольников).

2) Поскольку  то — средняя линия треугольника  Тогда, по свойству средней линии треугольника,  а значит,  Но так как  то

3) Кроме того,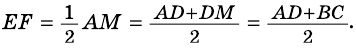

Пример:

Докажите, что отрезок средней линии трапеции, содержащийся между ее диагоналями, равен полуразности оснований.

Доказательство:

Пусть — средняя линия трапеции — точка пересечения и — точка пересечения и (рис. 110). Пусть  Докажем, что 

1) Так как и  то, по теореме Фалеса, -середина — середина  Поэтому — средняя линия треугольника  — средняя линия треугольника

Тогда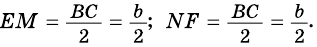

2) — средняя линия трапеции, поэтому

3)

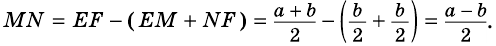
Пример:

В равнобокой трапеции диагональ делит острый угол пополам. Найдите среднюю линию трапеции, если ее основания относятся как 3 : 7, а периметр трапеции — 48 см.

Решение:

Пусть — данная трапеция, — ее средняя линия, 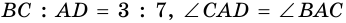(рис. 111).

1) Обозначим Тогда

2) (по условию). (как внутренние накрест лежащие при параллельных прямых  и и секущей  Поэтому  Следовательно, — равнобедренный, у которого (по признаку равнобедренного треугольника). Но (по условию), значит,

3) Учитывая, что  получим уравнение: откуда

4)    Тогда

Ответ. 15 см.

А еще раньше…

То, что средняя линия трапеции равна полусумме оснований, было известно еще древним египтянам; эту информацию содержал папирус Ахмеса (примерно XVII в. до н. э.).

О свойстве средней линии трапеции знали также и вавилонские землемеры; это свойство упоминается и в трудах Герона Александрийского (первая половина I в. н. э.).

Рекомендую подробно изучить предметы:

Геометрия Аналитическая геометрия Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

• Площадь трапеции
• Центральные и вписанные углы
• Углы и расстояния в пространстве
• Подобие треугольников
• Площадь параллелограмма
• Прямоугольник и его свойства
• Ромб и его свойства, определение и примеры
• Квадрат и его свойства

Свойства равнобокой трапеции

Рассмотрим некоторые важные свойства равнобокой трапеции.

1. В равнобокой трапеции углы при основании равны.

Доказательство:

1) Пусть в трапеции Проведем высоты трапеции и из вершин ее тупых углов и (рис. 70). Получили прямоугольник Поэтому

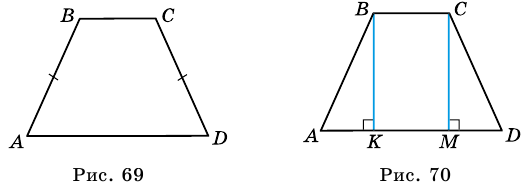
2)  (по катету и гипотенузе). Поэтому

3) Также Но поэтому и Следовательно,

2. Диагонали равнобокой трапеции равны.

Доказательство:

Рассмотрим рисунок 71. (как углы при основании равнобокой трапеции), — общая сторона треугольников и Поэтому (по двум сторонам и углу между ними). Следовательно,

Пример:

 — точка пересечения диагоналей равнобокой трапеции с основаниями и  (рис. 71). Докажите, что

Доказательство:

(доказано выше). Поэтому По признаку равнобедренного треугольника — равнобедренный. Поэтому Поскольку  и то  (так как ). 

Теорема (признак равнобокой трапеции). Если в трапеции углы при основании равны, то трапеция — равнобокая.

Доказательство:

1) Пусть в  углы при большем основании равны (рис. 70), то есть Проведем высоты и они равны.

2) Тогда (по катету и противолежащему углу). Следовательно, Таким образом, трапеция равнобокая, что и требовалось доказать. 

А еще раньше…

Термин «трапеция» греческого происхождения (по-гречески «трапед-зион» означает «столик», в частности столик для обеда; слова «трапеция» и «трапеза» — однокоренные).

В «Началах» Евклид под термином «трапеция» подразумевал любой четырехугольник, не являющийся параллелограммом. Большинство математиков Средневековья использовали термин «трапеция» с тем же смыслом.

Трапеция в современной трактовке впервые встречается у древнегреческого математика Посидония (I в.), но начиная только с XVIII в. этот термин стал общепринятым для четырехугольников, у которых две стороны параллельны, а две другие — не параллельны.

Следствие из Теоремы Фалеса

Следствием этой теоремы является теорема о средней линии треугольника.

Теорема 3

Средняя линия треугольника параллельна одной из сторон треугольника и также равна половине этой стороны.

Другим следствием теоремы Фалеса можно считать теорему о пропорциональных отрезках.

Теорема 4

Прямые, параллельные друг другу и пересекающие стороны угла, отсчитывают от сторон угла равные отрезки.

Из теоремы Фалеса также следуют следующие правила:

1. Медиана, проведенная к гипотенузе, будет равна половине гипотенузы.
2. Центром окружности, описывающей треугольник, является середина гипотенузы, а радиус окружности равен половине длины гипотенузы вписанного в окружность треугольника.

3. Признаки равнобедренной трапеции

На­пом­ним, что рав­но­бед­рен­ная тра­пе­ция – тра­пе­ция, у ко­то­рой бо­ко­вые сто­ро­ны равны. Рас­смот­рим свой­ства бо­ко­вой тра­пе­ции.

1.      Углы при ос­но­ва­нии рав­но­бед­рен­ной тра­пе­ции равны.

До­ка­за­тель­ство:

Вы­пол­ним стан­дарт­ное до­пол­ни­тель­ное по­стро­е­ние, ко­то­рое очень часто ис­поль­зу­ет­ся при ре­ше­нии раз­лич­ных задач на тра­пе­цию: про­ве­дём пря­мую  па­рал­лель­но бо­ко­вой сто­роне  (см. Рис. 4).

Рис. 4

 – па­рал­ле­ло­грамм.

От­сю­да сле­ду­ет, что: . Зна­чит, тре­уголь­ник  – рав­но­бед­рен­ный. А зна­чит, углы при его ос­но­ва­нии равны, то есть:  (по­след­ние два угла равны, как со­от­вет­ствен­ные при па­рал­лель­ных пря­мых ).

До­ка­за­но.

2.      Диа­го­на­ли рав­но­бед­рен­ной тра­пе­ции равны.

До­ка­за­тель­ство:

Для до­ка­за­тель­ства этого свой­ства вос­поль­зу­ем­ся преды­ду­щим. Дей­стви­тель­но, рас­смот­рим тре­уголь­ни­ки:  и  (см. Рис. 5.).

Рис. 5

 (по пер­во­му при­зна­ку ра­вен­ства тре­уголь­ни­ков: две сто­ро­ны и угол между ними).

Из этого ра­вен­ства сразу сле­ду­ет, что: .

До­ка­за­но.

Ока­зы­ва­ет­ся, что, как и в слу­чае с па­рал­ле­ло­грам­мом, у рав­но­бед­рен­ной тра­пе­ции свой­ства од­но­вре­мен­но яв­ля­ют­ся и при­зна­ка­ми. Сфор­му­ли­ру­ем и до­ка­жем эти при­зна­ки.

При­зна­ки рав­но­бед­рен­ной тра­пе­ции

1.      Дано:  – тра­пе­ция; .

До­ка­зать: 

До­ка­за­тель­ство:

До­ка­за­тель­ство дан­но­го при­зна­ка аб­со­лют­но ана­ло­гич­но до­ка­за­тель­ству со­от­вет­ству­ю­ще­го свой­ства. Про­ве­дём в тра­пе­ции  пря­мую  па­рал­лель­но сто­роне  (см. Рис. 6).

 – па­рал­ле­ло­грамм (две пары по­пар­но па­рал­лель­ных сто­рон).

 (со­от­вет­ствен­ные углы при па­рал­лель­ных пря­мых). От­ку­да, поль­зу­ясь усло­ви­ем, по­лу­ча­ем:  – рав­но­бед­рен­ный

Рис. 6

(равны углы при ос­но­ва­нии). Зна­чит:  (у па­рал­ле­ло­грам­ма про­ти­во­по­лож­ные сто­ро­ны равны).

До­ка­за­но.

2.      Дано:  – тра­пе­ция; .

До­ка­зать: .

До­ка­за­тель­ство:

Вы­пол­ним ещё одно стан­дарт­ное до­пол­ни­тель­ное по­стро­е­ние при ре­ше­нии задач с тра­пе­ци­ей: про­ве­дём через вер­ши­ну  пря­мую  па­рал­лель­но диа­го­на­ли  (см. Рис. 7).

Рис. 7

 – па­рал­ле­ло­грамм (две пары по­пар­но па­рал­лель­ных сто­рон).

 (со­от­вет­ствен­ные углы при па­рал­лель­ных пря­мых). Кроме того,  – рав­но­бед­рен­ный ( – по усло­вию;  – по свой­ству па­рал­ле­ло­грам­ма). А зна­чит: .

До­ка­за­но.

Свойства трапеции

Рассмотрим некоторые свойства трапеции.

1. Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.

Так как  то  (как сумма внутренних односторонних углов). Аналогично

2. Трапеция является выпуклым четырехугольником.

Поскольку то Аналогично Следовательно, трапеция — выпуклый четырехугольник. 

Высотой трапеции называют перпендикуляр, проведенный из любой точки основания трапеции к прямой, содержащей другое ее основание.

Как правило, высоту трапеции проводят из ее вершины. На рисунке 67 — высота трапеции

Трапецию называют прямоугольной, если один из ее углов -прямой. На рисунке 68 — прямоугольная трапеция Очевидно, что   является меньшей боковой стороной прямоугольной трапеции и ее высотой.

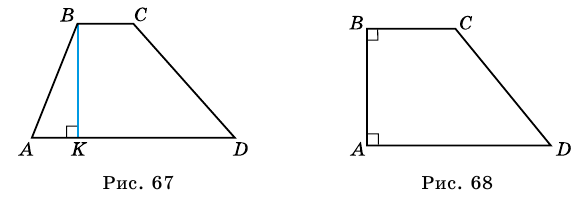
Трапецию называют равнобокой, если ее боковые стороны равны. На рисунке 69 — равнобокая трапеция

Теорема (об отрезке, соединяющем середины диагоналей трапеции)

Отрезок, соединяющий середины диагоналей трапеции, равен
полуразности ее оснований.

Доказательство

Рассмотрим трапецию $ABCD$, в которой точки $E$ и $F$ – это
середины диагоналей $AC$ и $BD$ соответственно.

Докажем, что $EF=\frac{AD-BC}{2}$.

По теореме Фалеса средняя линия трапеции $MN$ делит диагонали $AC$ и $BD$ пополам, то есть точки $E$ и $F$ лежат на средней линии.

Тогда $ME$ и $FN$ – это средние линии треугольников $\triangle ABC$ и $\triangle DBC$.

Следовательно, если обозначить $BC=2x$, то $ME=FN=x$.

Тогда $EF=\frac{2x+AD}{2}-x-x=\frac{AD-2x}{2}=\frac{AD-BC}{2}$.