Какое движение называют равномерным прямолинейным

Скорость, как главная характеристика движения

На примере стрелок часов – часовой, минутной и секундной – можно видеть разницу в движении. Хотя все эти три стрелки проходят за равные промежутки времени равные пути, а значит, все три движутся равномерно, двигаются они совершенно по-разному.

Для характеристики этой разницы введено понятие скорости.

Скорость равномерного движения тела равна пути, проходимому телом за единицу времени.

Рис. 2. Скорость равномерного движения.

То есть, для нахождения скорости надо найти отношение пройденного пути ко времени, за который этот путь был пройден. Поскольку при равномерном движении тело за любой равный промежуток времени проходит одно и то же время, то это отношение будет всегда одинаковым. Формула скорости равномерного движения:

$$v={s \over t},$$

где:

• $v$ – скорость;
• $s$ – путь;
• $t$ – время;

Таким образом, физический смысл скорости – это путь, проходимый телом в единицу времени.

Из этой же формулы можно найти размерность скорости. Поскольку расстояние в системе СИ измеряется в метрах, а время в секундах, то единицей скорости является:

$$v={s \over t}={м \over сек}$$

то есть, метры в секунду.

Хотя математически скорость может принимать любое значение, в реальном мире скорость любого материального тела не может быть больше скорости света в вакууме. Она равна примерно $3×10^8$ м/с.

Скорость

Найдем отношения путей к соответствующим промежуткам времени: \ \ \

Величина \(\frac{s}{Δt}\) — новая физическая величина, называемая скоростью. Обозначается скорость буквой \(v\).

Тогда для равномерного прямолинейного движения можно записать формулу: \ или \

Из формулы \(v = \frac{s}{Δt}\) следует, что скорость равномерного прямолинейного движения есть физическая величина, равная отношению пути, пройденного телом, к промежутку времени.

Из формулы \(v = \frac{s}{Δt}\) легко найти путь, пройденный за любой промежуток времени, и промежуток времени: \\

На примере с капельницей вы убедились, что при равномерном прямолинейном движении скорость является постоянной величиной.

При равномерном прямолинейном движении с увеличением промежутка времени увеличивается путь, но скорость остается постоянной.

Значит, скорость является характеристикой движения. Теперь можно дать еще одно определение равномерного прямолинейного движения, используя его характеристику — скорость: равномерное прямолинейное движение — это движение по прямой с постоянной скоростью.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?

1) 320 м/с
2) 80 м/с
3) 20 м/с
4) 0,05 м/с

2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?

1) 0,25 м
2) 6 м
3) 10 м
4) 150 м

3. Автомобиль «Рено» проезжает за 1 мин. путь 1,2 км. Автомобиль «Пежо» проезжает за 20 с путь 0,2 км. Сравните значения скорости «Рено» — ​\( v_1 \)​ и скорости «Пежо» — \( v_2 \).

1) ​\( v_1=v_2 \)​
2) ​\( v_1=2v_2 \)​
3) \( 2v_1=v_2 \)
4) \( 1,2v_1=10v_2 \)

4. На рисунке приведена столбчатая диаграмма. На ней представлены значения пути, которые при равномерном движении пролетают за одно и то же время муха (1) и воробей (2). Сравните их скорости ​\( v_1 \)​ и \( v_2 \).

1) ​\( v_1=v_2 \)​
2) ​\( v_1=2v_2 \)​
3) \( 3v_1=v_2 \)
4) \( 2v_1=v_2 \)

5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен

1) 20 м
2) 40 м
3) 80 м
4) 160 м

6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен

1) 0,1 м/с
2) 10 м/с
3) 20 м/с
4) 40 м/с

7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости ​\( v_1 \)​, \( v_2 \) и \( v_3 \) движения этих тел.

1) ​\( v_1=v_2=v_3 \)​
2) \( v_1>v_2>v_3 \)​
3) \( v_1<v_2<v_3 \)​
4) ​\( v_1=v_2 \), \( v_3<v_1 \)

8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?

9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?

1) 9,8 м
2) 6 м
3) 4 м
4) 2 м

10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид

1) ​\( x=1t \)​ (м)
2) \( x=2+3t \) (м)
3) \( x=2-1t \) (м)
4) \( x=4+2t \) (м)

11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ВЕЛИЧИНА
A) перемещение
Б) время
B) скорость

ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА
1) зависит
2) не зависит

12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.

1) тело двигалось все время в одну сторону
2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался
3) проекция скорости тела все время была положительной
4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной
5) в момент времени 4 с тело остановилось

Часть 2

13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?

Равномерное прямолинейное движение: скорость и уравнение движения

Путь и перемещение при равномерном прямолинейном движении

Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.

Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:

равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.

Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.

Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см

рисунок 8). Радиус-вектор, проведенный в точку A обозначим r, а радиус-вектор в точку Б обозначим r1. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.

Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении

Тогда скорость движения (v) будет вычисляться по формуле:

Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.

Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r₁ — r. Тогда выражение для скорости можно переписать в виде:

Из этого выражения следует:

r₁ = r + v*t.

Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:

r= r + v*t.

Данное уравнение является уравнением движения при прямолинейном равномерном движении.

*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t₁, где t – конечный момент времени, t₁ – начальный. Если же начальный момент времени совпадает с началом отсчета t₁ = 0, то △t = t – 0 = t_.

Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.

Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.

r_x = r_0x + v_x*t;

r_y = r_0y + v_y*t;

r_z = r_0z + v_z*t.

В этих выражениях r_0x, r_0y, r_0z и v_x, v_y, v_z– это компоненты изначальных векторов r и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:

r_x = r_0x + v_x*t;
r_y = r_0y + v_y*t;
r_z = r_0z + v_z*t.

Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.

В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х) и конечной (х₁) точки на ось ОХ.

Рисунок 9 – Перемещение тела в координатном представлении

Уравнение координаты (х) движения будет выглядеть:

x(t) = x+ v*t.

А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:

S(t) = S + v*t.

Если точка начала двигаться из начала отсчета S = 0, можно переписать эту формулу в виде:

S(t) = v*t.

Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:

Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.

Итак, для начала приведем все единицы измерения к СИ:

x = 3 см = 0,03 м.

Теперь можно записывать уравнение для координаты х:

x(t) = x+ v*t = 0,03 + 5*t.

Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:

x(2) = 0,03 + 5*2 = 10, 03.

А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2)  = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:

S = x(2) – x = 10, 03 – 0,03 = 10 м.

А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?

Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:

x(t) = x- v*t = 0,03 — 5*t.

Топ вопросов за вчера в категории Физика

Физика 19.06.2023 23:44 3090 Трухман Дарья

6. По графику зависимости скорости равномерно дви- жущегося тела от времени (рис. 43) определите с

Ответов: 1

Физика 28.09.2023 20:06 4828 Копылова Алёна

3) Предложите единицы скорости, не указанные в параграфе.7 класс Физика​

Ответов: 2

Физика 05.06.2023 05:32 1966 Блок Богдана

7. По графикам зависимости пути от времени (рис. 44) двух тел, движущихся равномерно, определите,

Ответов: 1

Физика 20.06.2023 14:02 3482 Ашкенова Дарига

Скоростной поезд за 10 минут проходит путь, равны 40 км. Определить его среднюю скорость.

Ответов: 1

Физика 29.04.2023 12:23 4789 Парамонов Александр

К неподвижном у телу массой 20 кг приложили постоянную силу 6Н .Какую скорость приобретёт тело за15с

Ответов: 2

Физика 08.11.2018 21:44 185 Вологдина Лиза

ФИЗИКА!!потенциальная энергия взаимодействия с землей гири массой 5 кг увеличилась на 75 дж.На сколь

Ответов: 1

Физика 20.06.2023 01:53 1247 Милованова Виктория

постройте графики зависимости пути от времени для тел, одно из которых движется с постоянной скорост

Ответов: 1

Физика 09.01.2020 05:53 2468 Хлыбов Глеб

С какой скоростью плывет лосось, если за 5 секунд он проплыл 30 метров

Ответов: 2

Физика 03.06.2023 02:50 505 Земляной Дима

Первую половину пути из Москвы в Подольск автомобиль ехал со скоростью 90 км ч а оставшийся путь 20

Ответов: 2

Физика 21.06.2023 05:58 2119 Кулик Станислав

при полном сгорании 6кг топлива выделилось количество теплоты 2,76*10 в 8 степени. О каком топливе и

Ответов: 1

Основные понятия и законы динамики

Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой

Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.

Принцип относительности Галилея:во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законамМасса — это мера инертности телаСила — это количественная мера взаимодействия тел.

Второй закон Ньютона:Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F{→} = m⋅a{→}$

Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.

Третий закон Ньютона: Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1{→} = -F_2{→} $

III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.

Закон Гука записывают в виде
где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.

При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле
где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.

Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значенияГравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.

Закон всемирного тяготения:Весом телаСила тяжестиНевесомостьюИскусственный спутник ЗемлиПервая космическая скорость

1.3. Основные понятия и законы статики и гидростатики

устойчивое, неустойчивое и безразличное.устойчивое равновесие.неустойчивое положениебезразличноеПлечом силыУсловие равновесия рычага:Давлениемзакон Паскаля:Гидравлический прессA1 = A2.силой Архимедазакон Архимеда_{жидкпогр}Условие плавания тела

1.4. Законы сохранения

Импульсом телаимпульсом силы.закон сохранения импульсаМеханической работойМощностьэнергией.кинетическую и потенциальную.кинетической энергией.потенциальной энергией.Энергия сжатой пружины:механическую энергию.закон сохранения механической энергии

1.5. Механические колебания и волны

КолебаниямиГармоническими колебаниямиамплитудой колебанийПериодом TЧастотой периодических колебаний-1Математическим маятникомПериод колебаний математического маятникаПериод колебаний груза на пружинеРаспространение колебаний в упругих средах.поперечнойпродольнойДлиной волныЗвуковыми волнами

Определение скорости равномерного прямолинейного движения

Скорость равномерного прямолинейного движения — это величина, определяющая скорость изменения положения тела в пространстве за единицу времени. В отличие от скорости переменного движения, где скорость может меняться со временем, скорость равномерного прямолинейного движения остается постоянной.

Скорость равномерного прямолинейного движения измеряется в единицах длины, например, метрах в секунду (м/с) или километрах в час (км/ч). Она может быть положительной, если тело движется в положительном направлении оси координат, и отрицательной, если тело движется в отрицательном направлении.

Для определения скорости равномерного прямолинейного движения можно использовать следующую формулу:

Символ	Описание
v	скорость равномерного прямолинейного движения
s	путь, пройденный телом за определенный период времени
t	время, за которое тело преодолело заданный путь

Формула для определения скорости равномерного прямолинейного движения:

v = s / t

Например, если тело преодолело путь длиной 100 метров за 10 секунд, то его скорость равномерного прямолинейного движения будет:

v = 100 м / 10 с = 10 м/с

Таким образом, скорость равномерного прямолинейного движения определяется отношением пройденного пути к затраченному времени и показывает, как быстро тело движется в пространстве.

Прямолинейное равномерное движение и его характеристики

Наиболее простым для расчетов представляется прямолинейное равномерное движение. Равномерное означает одинаковое расстояние за равные промежутки времени. Прямолинейное значит по прямой траектории.

И тогда перемещение в векторном виде найдется, как произведение скорости на время:

Для определения числовых значений используют проекции (в формулу вместо вектора число подставлять нельзя): s_x = v_xt.

Часто при решении задач в записи индексы опускают, и расчетная формула принимает простой вид: s = vt.

Эта формула известна еще из математики до изучения физики. Но в ней буквой s в математических задачах обозначался путь, пройденный движущимся объектом, а теперь речь идет о перемещении. Ошибки здесь нет.

Для наглядного представления движения используются графики движения. Например, график зависимости модуля вектора скорости от времени.

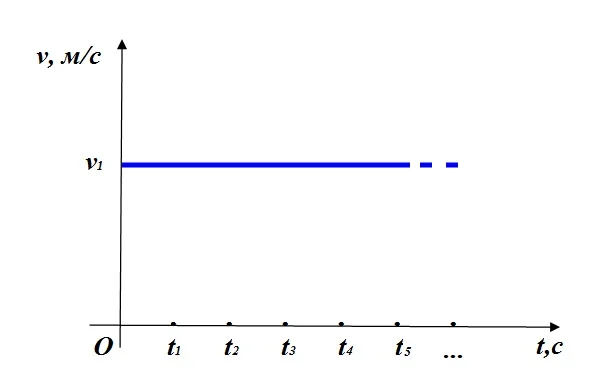
При построении графика по горизонтальной оси откладывают время t, по вертикальной – скорость v. После запятой указываются единицы измерения.

При равномерном движении с течением времени скорость не меняется, и поэтому на графике указанное значение скорости v₁ постоянно. В результате график представлен в виде прямой, параллельной оси Оt.

А теперь интересный момент геометрической интерпретации модуля перемещения.

Пусть наблюдение за движением тела велось в течение времени t₅ тогда численное значение перемещения s = v₁t₅.

Но с точки зрения геометрии с помощью произведения v₁t₅ находится площадь S прямоугольника со сторонами Ov₁ и Ot₅.

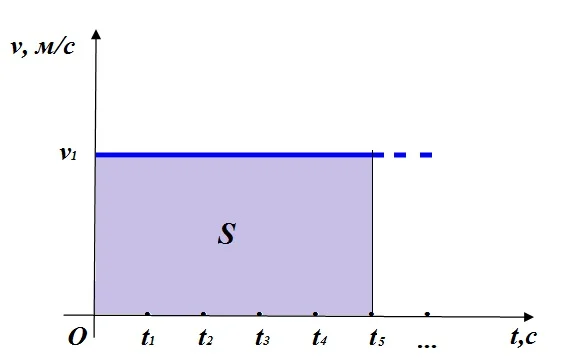
Получается такая связь:

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. Чему равна проекция скорости равномерно движущегося автомобиля, если проекция его перемещения за 4 с равна 80 м?

1) 320 м/с 2) 80 м/с 3) 20 м/с 4) 0,05 м/с

2. Чему равен модуль перемещения мухи за 0,5 мин., если она летит со скоростью 5 м/с?

1) 0,25 м 2) 6 м 3) 10 м 4) 150 м

3. Автомобиль «Рено» проезжает за 1 мин. путь 1,2 км. Автомобиль «Пежо» проезжает за 20 с путь 0,2 км. Сравните значения скорости «Рено» — ​ \( v_1 \) ​ и скорости «Пежо» — \( v_2 \) .

1) ​ \( v_1=v_2 \) ​ 2) ​ \( v_1=2v_2 \) ​ 3) \( 2v_1=v_2 \) 4) \( 1,2v_1=10v_2 \)

4. На рисунке приведена столбчатая диаграмма. На ней представлены значения пути, которые при равномерном движении пролетают за одно и то же время муха (1) и воробей (2). Сравните их скорости ​ \( v_1 \) ​ и \( v_2 \) .

1) ​ \( v_1=v_2 \) ​ 2) ​ \( v_1=2v_2 \) ​ 3) \( 3v_1=v_2 \) 4) \( 2v_1=v_2 \)

5. На рисунке приведён график зависимости модуля скорости равномерного движения от времени. Модуль перемещения тела за 2 с равен

1) 20 м 2) 40 м 3) 80 м 4) 160 м

6. На рисунке приведён график зависимости пути, пройденного телом при равномерном движении от времени. Модуль скорости тела равен

1) 0,1 м/с 2) 10 м/с 3) 20 м/с 4) 40 м/с

7. На рисунке приведены графики зависимости пути от времени для трёх тел. Сравните значения скорости ​ \( v_1 \) ​, \( v_2 \) и \( v_3 \) движения этих тел.

1) ​ \( v_1=v_2=v_3 \) ​ 2) \( v_1>v_2>v_3 \) ​ 3) \( v_1 ​ 4) ​ \( v_1=v_2 \) , \( v_3

8. Какой из приведённых ниже графиков представляет собой график зависимости пути от времени при равномерном движении тела?

9. На рисунке приведён график зависимости координаты тела от времени. Чему равна координата тела в момент времени 6 с?

1) 9,8 м 2) 6 м 3) 4 м 4) 2 м

10. Уравнение движения тела, соответствующее приведённому в задаче 9 графику, имеет вид

1) ​ \( x=1t \) ​ (м) 2) \( x=2+3t \) (м) 3) \( x=2-1t \) (м) 4) \( x=4+2t \) (м)

11. Установите соответствие между величинами в левом столбце и зависимостью значения величины от выбора системы отсчёта в правом столбце. В таблице под номером элемента знаний левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ВЕЛИЧИНА A) перемещение Б) время B) скорость

ЗАВИСИМОСТЬ ОТ ВЫБОРА СИСТЕМЫ ОТСЧЁТА 1) зависит 2) не зависит

12. На рисунке приведён график зависимости координаты тела от времени. Какие выводы можно сделать из анализа графика? Укажите два правильных ответа.

1) тело двигалось все время в одну сторону 2) в течение четырёх секунд модуль скорости тела уменьшался, а затем увеличивался 3) проекция скорости тела все время была положительной 4) проекция скорости тела в течение четырёх секунд была положительной, а затем — отрицательной 5) в момент времени 4 с тело остановилось

Часть 2

13. Два автомобиля движутся друг за другом равномерно и прямолинейно: один со скоростью 20 м/с, другой — со скоростью 15 м/с. Через какое время второй автомобиль догонит первый, если в начальный момент времени расстояние между ними равно 100 м?

Равномерное прямолинейное движение в физике — формулы и определения с примерами

Равномерное прямолинейное движение:

Вы изучали равномерное прямолинейное движение, познакомились с понятием «скорость». Скалярной или векторной величиной является скорость? Каковы закономерности равномерного прямолинейного движения?

Вы знаете, что движение, при котором за любые равные промежутки времени тело проходит одинаковые пути, называется равномерным. В каком случае одинаковыми будут не только пути, но и перемещения?

Проделаем опыт. Проследим за падением металлического шарика в вертикальной трубке, заполненной вязкой жидкостью (например, густым сахарным сиропом) (рис. 43). Будем отмечать положение шарика через равные промежутки времени. Опыт показывает, что за равные промежутки времени, например за

Сделаем вывод. При равномерном прямолинейном движении тело за любые равные промежутки времени совершает одинаковые перемещения и проходит одинаковые пути.

В 7-м классе вы находили скорость равномерного движения тела как отношение пути к промежутку времени, за который путь пройден: Это отношение показывает, как быстро движется тело, но ничего не говорит о направлении движения. Чтобы скорость характеризовала и быстроту движения, и его направление, ее определяют через перемещение.

Скорость равномерного прямолинейного движения — это величина, равная отношению перемещения к промежутку времени, за который оно совершено:

Из равенства (1) следует, что скорость — векторная физическая величина. Ее модуль численно равен модулю перемещения за единицу времени, а направление совпадает с направлением перемещения (т. к. ).

Отношение для всех участков движения на рисунке 43 одинаково: Значит, скорость равномерного прямолинейного движения постоянна: с течением времени не изменяется ни ее модуль, ни ее направление.

Из формулы (1) легко найти перемещение:

и путь (равный модулю перемещения ):

А как определить положение равномерно и прямолинейно движущегося тела в любой момент времени Рассмотрим пример. Автомобиль движется с постоянной скоростью по прямолинейному участку шоссе (рис. 44).

Автомобиль рассматриваем как материальную точку. Из формулы (2) находим проекцию перемещения автомобиля на ось Ох:

Согласно рисунку 44 за время автомобиль совершил перемещение Подставляя в равенство (4), получим:

Приняв запишем формулу для координаты автомобиля:

Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.

Зависимость координаты движущегося тела от времени называется кинематическим законом движения. Формула (5) выражает кинематический закон равномерного прямолинейного движения.

Для измерения скорости используются специальные приборы. В автомобилях имеется спидометр (рис. 45), на самолетах — указатель скорости. Эхолокаторы измеряют скорость тел, движущихся под водой, а радиолокаторы (радары) — в воздухе и по земле. Сотрудники службы дорожного движения с помощью портативного радара с видеокамерой (рис. 46) регистрируют скорость транспортных средств.

Для любознательных:

Скорости движения могут сильно отличаться. За одну секунду черепаха может преодолеть несколько сантиметров, человек — до 10 м, гепард — до 30 м, гоночный автомобиль — около 100 м.

Около 8 км за секунду пролетает по орбите спутник Земли (рис. 47). Но даже скорости космических кораблей «черепашьи» по сравнению со скоростью микрочастиц в ускорителях. В современном ускорителе (рис. 48) электрон за одну секунду пролетает почти 300 000 км!

Главные выводы:

1. При равномерном прямолинейном движении за любые равные промежутки времени тело совершает одинаковые перемещения.
2. Скорость равномерного прямолинейного движения постоянна: с течением времени не изменяется ни ее модуль, ни ее направление.
3. При равномерном прямолинейном движении тела модуль перемещения равен пути, пройденному за тот же промежуток времени.
4. Координата равномерно и прямолинейно движущегося тела линейно зависит от времени.

Пример решения задачи:

Кинематический закон прямолинейного движения лодки но озеру вдоль оси Ох задан уравнением где

Определите: 1) проекцию скорости лодки 2) координату лодки в момент времени 3) проекцию перемещения лодки на ось Ох и путь, пройденный лодкой за время от момента до момента

Решение

Сделаем рисунок к задаче.

По условию задачи координата лодки линейно зависит от времени. Значит, лодка движется равномерно. Сравнив получим

Найдем

Из рисунка 49: проекция перемещения

Ответ:

Координаты движущегося тела

Используя вектор перемещения, можно найти положение тела. Но чаще необходимо не найти, где находится тело, а вычислить его координаты. Вычисления производятся не с векторами, а со скалярными величинами, соответствующими векторам. Такими величинами являются проекции векторов на оси координат, модули векторов или модули проекций. Эти величины не имеют направления и представлены положительными и отрицательными числами.

Делать проекцию вектора на оси нужно с помощью проведения перпендикуляров. Из начала и конца вектора на ось опускается перпендикуляр. Отрезок между основаниями перпендикуляров и будет являться проекцией вектора на соответствующую ось.

Пусть точка А(х₁; у₁) – начало вектора, точка В(х₂; у₂) – конец вектора. Проекцией вектора АВ на ось Ох станет отрезок х₁х₂, на ось Оу – отрезок у₁у₂.

Числовое значение проекции равно разности координат конца и начала вектора.

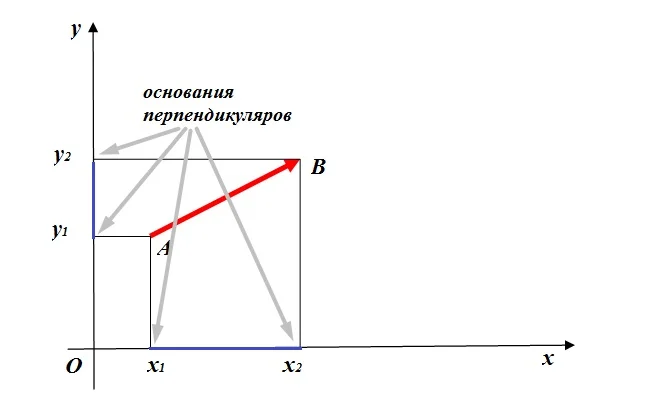
Следует обратить внимание, что если х2 – х1 ˃ 0 (y2 – y1 ˃ 0), то проекции на оси будут положительными

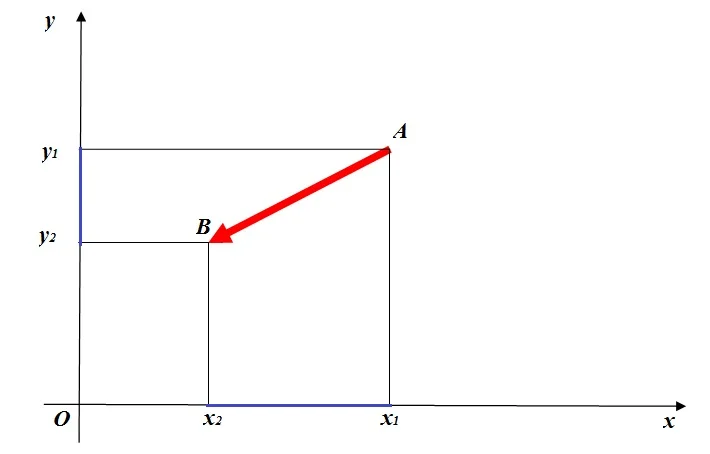
Если х₂ – х₁ ˂ 0 (у₂ – у₁ ˂ 0), проекции вектора на оси отрицательны.

Как вычислить координаты тела, зная вектор перемещения? Необходимо следовать примерно такому плану:

• 1) Пусть перемещением является вектор s.
• 2) Координаты начала вектора х₁ и у₁.
• 3) Координаты конца вектора х₂ и у₂.

Проекции на оси s_x и s_y.

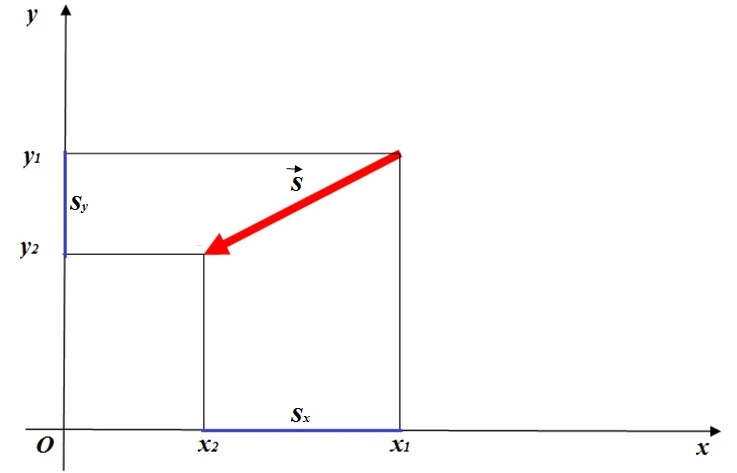
• Проекции вычисляются по формулам s_x = x₂ – x₁ и s_y = y₂ – y₁.  
• Из этих формул находятся координаты конца вектора перемещения (то есть координаты тела в некоторый момент времени)

Для упрощения графического представления и вычислений координатные оси выбирают так, чтобы направление одной оси (чаще всего Ох) совпадало с направлением перемещения. И тогда вторая ось практически не нужна.

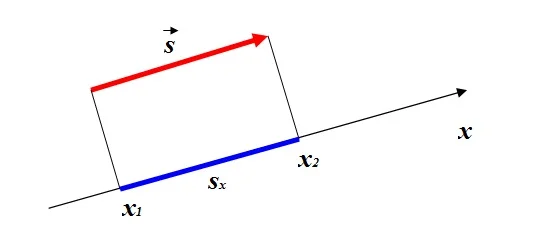
В таком случае длина (модуль) вектора перемещения и длина проекции его на ось равны.

Примеры решения задач

Однако не при любом виде движения можно использовать данную формулу для определения перемещения. Существует ряд особенностей (рассмотрены ниже, в виде примеров), в которых действия имеют иной характер.

Задача 1

Каков модуль и каково направление скорости тела, если известно, что движение равномерно и происходит вдоль оси OX. С начала движения прошло 4 секунды, а координата изменилась с 5м до -3м.

Решение

Выше было рассмотрено, что отражением модуля и направления вектора являются проекции на оси координат. Поскольку движение характеризуется равномерностью, то проекцию скорости на ось абсцисс можно определить по следующей формуле:

Проекция может иметь отрицательный знак. В таком случае скорость точки иметь направление, противоположное положительному по оси OX. Модуль скорости \(V=|Vx|=|-2м/с|=2м/с.\)

Задача 2

Расстояние между пунктами A и B по прямой линии 20 км. Навстречу друг другу из этих пунктов одновременно выехали два автомобиля. Первый имел скорость 50 км/ч, второй — 60 км/ч.

Необходимо определить места положения автомобилей относительно пункта А через полчаса с момента начала движения, а также на каком расстоянии они будут друг от друга в этот момент.

Решение.

Автомобили совершают движения, которые можно выразить формулами:

Спустя полчаса (0,5ч), их положение математически можно выразить так:

Один из автомобилей достигнет точки C, отдаленной от старта движения на 25 км вправо от A. Второй автомобиль достигнет точки D, которая отдалена влево на 10 км. Таким образом, модуль расстояния составит разность их координат:

\(S=|X2-X1| =|-10км-25км|=35км\)

Соответственно пройденные расстояния можно найти по формулам:

\(S1=V1t=50 км/ч*0,5ч=25км\)

\(S2=V2t=60 км/ч*0,5ч=30км\)

Задача 3

Автомобиль выехал из пункта A в пункт B со скоростью V1. Через время t0 пункт B покинул второй автомобиль и направился в том же направлении. Его скорость составила V2. Расстояние между пунктами обозначаем S. Где будет находиться место встречи автомобилей (выразить через пункт B)? Какое время пройдет до их встречи (выразить через первый автомобиль)?

Решение

Задача № 3

Автомобиль выехал из пункта A в пункт B со скоростью V₁. Через время t пункт B покинул второй автомобиль и направился в том же направлении. Его скорость составила V₂.

Расстояние между пунктами обозначаем S.

Где будет находиться место встречи автомобилей (выразить через пункт B)? Какое время пройдет до их встречи (выразить через первый автомобиль)?

Решение

При встрече автомобилей их координаты будут равны: X₁=X₂=X_в

В целом уравнения движения в данном случае выглядят так:

X₁=V₁t

X₂=S+V₂(t-t)

Производя математические действия, получаем:

V₁t_в=S+V₂(t_в-t)

Вероятно, V₁>V₂, S>V₂t

Место встречи автомобилей можно найти по формуле: