Знаки проекций векторов перемещения: понимание и применение

Как определяют проекцию вектора на ось

Проекция вектора на ось — это длина отрезка между проекциями начала и конца вектора, взятая со знаком «+» или «-». Знак «+» берут, если угол между вектором и осью острый, а знак «-» — если угол тупой.

На рисунке 25 проекция вектора на ось Ох обозначена через а проекция вектора — через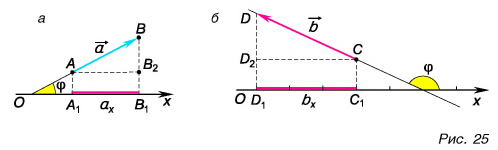
Проекция — число положительное, т. к. угол на рисунке 25, а — острый. Проекция — число отрицательное т. к. угол на рисунке 25, б — тупой.

А если вектор перпендикулярен оси? Тогда его проекция на эту ось равна нулю (рис. 26).

Проекцию вектора можно выразить через его модуль и угол между вектором и осью.

Рассмотрим треугольник на рисунке 25, а. Его гипотенуза катет а угол между ними равен  Следовательно,

Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между вектором и осью.

Это правило справедливо при любых углах между вектором и осью. Подтвердите это с помощью рисунков 25 и 26.

Обратим внимание на еще одно важное свойство проекций: проекция суммы векторов на ось равна сумме их проекций на эту ось

С помощью рисунка 27, а, б убедитесь, что из векторного равенства следует равенство для проекций: Не забывайте о знаках проекций.

Можно ли найти модуль и направление вектора по его проекциям на координатные оси

Рассмотрим вектор лежащий в плоскости (рис. 28). Его проекции на оси определим из рисунка:

Модуль вектора находим по теореме Пифагора из треугольника ACD: Разделив на получим: По значению косинуса находим угол

Таким образом, вектор, лежащий в заданной плоскости, полностью определяется двумя проекциями на оси координат.

Вектор в пространстве определяется тремя проекциями: (рис. 29).
 

Главные выводы:

1. Проекция вектора на ось — это длина отрезка, заключенного между проекциями начала и конца вектора на эту ось, взятая со знаком «+» или «-».
2. Если угол между вектором и осью острый, то его проекция на эту ось положительна, если угол тупой — отрицательна, если прямой — равна нулю.
3. Проекция вектора на ось равна произведению его модуля на косинус угла между вектором и осью.
4. Проекция суммы векторов на ось равна сумме их проекций на эту ось.

Пример №1

1. Определите сумму и разность взаимно перпендикулярных векторов (рис. 30). Найдите модули векторов суммы и разности

Решение

Сумму векторов  находим по правилу треугольника (рис. 31, а) или параллелограмма (рис. 31, б). Так как векторы взаимно перпендикулярны, модуль вектора  находим по теореме Пифагора:  Разность векторов  определим по правилам вычитания векторов (рис. 32, а, б).

Модуль вектора находим аналогично:

Ответ:

Заказать решение задач по физике

Пример №2

Выразите вектор  через векторы (рис. 33). Как связаны между собой проекции этих векторов на оси Ох и Оу?

Решение

По правилу треугольника находим: Отсюда Определив координаты начальных и конечных точек векторов находим проекции этих векторов: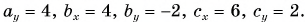  

Вычислением убедимся, что проекции векторов связаны теми же равенствами, что и сами векторы: 

Ответ:

Рекомендую подробно изучить предметы:

Физика Атомная физика Ядерная физика Квантовая физика Молекулярная физика

Ещё лекции с примерами решения и объяснением:

• Путь и перемещение
• Равномерное прямолинейное движение
• Прямолинейное неравномерное движение 
• Прямолинейное равноускоренное движение
• Колебательное движение
• Физический и математический маятники
• Пружинные и математические маятники
• Скалярные и векторные величины и действия над ними

Равномерное прямолинейное движение: скорость и уравнение движения

Путь и перемещение при равномерном прямолинейном движении

Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.

Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:

равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.

Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.

Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см

рисунок 8). Радиус-вектор, проведенный в точку A обозначим r, а радиус-вектор в точку Б обозначим r1. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.

Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении

Тогда скорость движения (v) будет вычисляться по формуле:

Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.

Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r₁ — r. Тогда выражение для скорости можно переписать в виде:

Из этого выражения следует:

r₁ = r + v*t.

Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:

r= r + v*t.

Данное уравнение является уравнением движения при прямолинейном равномерном движении.

*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t₁, где t – конечный момент времени, t₁ – начальный. Если же начальный момент времени совпадает с началом отсчета t₁ = 0, то △t = t – 0 = t_.

Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.

Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.

r_x = r_0x + v_x*t;

r_y = r_0y + v_y*t;

r_z = r_0z + v_z*t.

В этих выражениях r_0x, r_0y, r_0z и v_x, v_y, v_z– это компоненты изначальных векторов r и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:

r_x = r_0x + v_x*t;
r_y = r_0y + v_y*t;
r_z = r_0z + v_z*t.

Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.

В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х) и конечной (х₁) точки на ось ОХ.

Рисунок 9 – Перемещение тела в координатном представлении

Уравнение координаты (х) движения будет выглядеть:

x(t) = x+ v*t.

А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:

S(t) = S + v*t.

Если точка начала двигаться из начала отсчета S = 0, можно переписать эту формулу в виде:

S(t) = v*t.

Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:

Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.

Итак, для начала приведем все единицы измерения к СИ:

x = 3 см = 0,03 м.

Теперь можно записывать уравнение для координаты х:

x(t) = x+ v*t = 0,03 + 5*t.

Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:

x(2) = 0,03 + 5*2 = 10, 03.

А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2)  = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:

S = x(2) – x = 10, 03 – 0,03 = 10 м.

А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?

Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:

x(t) = x- v*t = 0,03 — 5*t.

Что такое проекция начальной скорости

Проекция начальной скорости — это значение скорости тела в определенном направлении в начальный момент времени. Она определяется как компонента начальной скорости вдоль выбранного направления.

В физике проекция начальной скорости играет важную роль при решении задач, связанных с движением тела. За частую, движение тела может происходить в разных направлениях, и для того, чтобы определить его дальнейшее движение, нужно знать скорость тела в каждом из них. Именно для этого и вводится понятие проекции начальной скорости.

Обозначается проекция начальной скорости буквой v с индексом, указывающим на направление проекции. Например, v_x — проекция начальной скорости на ось x, v_y — проекция начальной скорости на ось y и т.д.

Кроме того, проекция начальной скорости может быть положительной или отрицательной в зависимости от направления. Направление положительной проекции указывается заранее и следует за системой отсчета.

В заключение, знание проекции начальной скорости — это ключевой момент в решении задач, связанных с движением тела. Она позволяет определить параметры движения тела в нужном направлении и значительно ускоряет процесс расчетов.

Проекция начальной скорости

Начальная скорость — это скорость тела в начальный момент времени

В физике важное значение имеет вектор начальной скорости, который имеет направление и величину. Если тело движется в плоскости, то можно выделить его проекцию на координатные оси

Проекция начальной скорости — это скорость тела, проектированная на координатную ось. Проекция может иметь положительное и отрицательное значение в зависимости от направления движения тела.

Проекция начальной скорости является важной характеристикой движения, так как она позволяет определить зависимость пройденного пути от времени и изменение скорости тела во время движения. К примеру, если тело движется под углом к оси проекции, то проекция начальной скорости будет являться составляющей движения, в направлении оси

Эта характеристика помогает определить траекторию движения тела и описать его положение относительно других тел в пространстве

К примеру, если тело движется под углом к оси проекции, то проекция начальной скорости будет являться составляющей движения, в направлении оси. Эта характеристика помогает определить траекторию движения тела и описать его положение относительно других тел в пространстве.

Для расчета проекции начальной скорости можно использовать формулу проекции вектора:

v_x=vcosα,

где v — вектор начальной скорости, α — угол между вектором скорости и осью проекции.

Как влияет проекция скорости на движение тела

Проекция начальной скорости является соответствующей компонентой общей скорости тела, направленной вдоль определенной оси координат. Она играет важную роль в физических расчетах и позволяет определить направление, скорость и ускорение движения тела.

Влияние проекции скорости на движение тела зависит от многих факторов, таких как масса тела, его форма, сила трения и среда, в которой оно движется. Например, при движении тела по наклонной плоскости, его проекция скорости уменьшается, поскольку кинетическая энергия тела переходит в потенциальную энергию в поле силы тяжести.

Также проекция начальной скорости может влиять на траекторию движения тела, позволяя определить угол броска и дальность полета. Например, при броске мяча под углом к горизонту его проекция скорости направлена по касательной к траектории, что позволяет мячу пролететь максимальное расстояние до падения на землю.

Таким образом, знание проекции начальной скорости позволяет предсказывать и контролировать движение тела в различных условиях, что широко используется в научных и инженерных расчетах, а также в спортивной практике.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​\( t \)​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​\( t \)​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью \( t \), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью \( t \), тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время \( t \). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​\( x=x(t) \)​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Перемещение и описание движения

Система отсчёта используется для того, чтобы определить положение тела в пространстве в некоторый момент времени. В случае когда тело движется, возникает задача вычисления его координат в некоторые моменты времени.

ПРОЕКЦИИ ПЕРЕМЕЩЕНИЯ НА КООРДИНАТНЫЕ ОСИ

Если известен вектор перемещения тела, то при расчетах, как правило, используют не координаты вектора, как такового, а его проекции на оси координат. Если опустить перпендикуляры из начала и конца вектора перемещения s на координатную ось X, то получится отрезок s_x, который называют проекцией перемещения. При этом проекция вектора на ось считается положительной, если координата конца вектора перемещения оказывается больше координаты его начала. В противном случае проекция считается отрицательной.

Если вектор и ось параллельны, то длина вектора равна его проекции на эту ось.

При решении многих задач необходимо уметь находить проекции вектора перемещения на координатные оси. Если (х; у) и (х; у) — координаты начала и конца вектора, то его проекции на оси абсцисс и ординат будут равны соответственно

s_x = x – x,     (1)s_y = y – y

Зная проекции вектора перемещения, можно найти его длину (модуль) по теореме Пифагора:

ОПРЕДЕЛЕНИЕ КООРДИНАТ ДВИЖУЩЕГОСЯ ТЕЛА И ЕГО ПЕРЕМЕЩЕНИЯ

Если тело движется прямолинейно, то траектория его движения совпадает с перемещением. При этом пройденный телом путь равен значению модуля вектора перемещения.

А как описать движение тела в более сложном случае? На рисунке представлен график движения самолёта. Сначала он набирал высоту, двигаясь из точки А в точку В, затем двигался на одной и той же высоте (до точки С) и, наконец, приземлился в точке D. На какой высоте проходил полёт? Высоте полёта соответствуют координаты по оси OY, значит, в точке В самолёт набрал высоту 3 км.

Теперь ответим на вопрос: какой путь проделал самолёт на этой высоте? Проекция перемещения s_2x = 80 — 20 = 60 км.

Так как всё это время самолёт двигался параллельно оси ОХ, длина вектора перемещения равна его проекции на эту ось. Следовательно, модуль перемещения самолёта из точки В в точку С равен 60 км. Этому же значению равен и путь самолёта из точки В в точку С.

И наконец, определим дальность полёта самолёта. Для этого нам надо найти модуль перемещения самолёта из точки А в точку D: |s| = s_x = 100 — 0 = 100 км.

Таким образом, при помощи перемещения и его проекций мы описали сложное движение самолёта.

ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ РАВНОМЕРНОМ ПРЯМОЛИНЕЙНОМ ДВИЖЕНИИ

Так как при прямолинейном движении пройденный телом путь равен значению модуля вектора перемещения, мы можем сказать, что скоростью равномерного прямолинейного движения называют векторную величину, равную отношению перемещения тела ко времени, за которое это перемещение произошло. При равномерном прямолинейном движении векторы скорости и перемещения направлены в одну сторону. Зная скорость равномерного движения, можно найти перемещение тела за любой промежуток времени:

Поскольку скорость υ является векторной величиной, её тоже можно изобразить графически. Обозначим её проекцию на координатную ось υ_x. Если направление координатной оси совпадает с направлением движения тела, то для расчёта перемещения тела можно использовать формулу

УРАВНЕНИЕ ДВИЖЕНИЯ

Уравнение зависимости координаты тела от времени называют уравнением движения.

Пусть тело совершило перемещение s. Направим координатную ось X по направлению перемещения тела. Обозначим начальную координату тела х, а конечную координату тела х. Тогда по формуле (1) s_x = х – х.

Но по формуле (3) s_x = υ_xt. Следовательно,

Таким образом, координату тела при равномерном прямолинейном движении в любой момент времени можно определить, если известны его начальная координата и проекция скорости движения на ось X.

Ранее при решении задач мы использовали формулу s = υt без стрелочек. Почему? Символом s здесь обозначался путь, пройденный телом, а символом и — модуль скорости. Теперь нам известно, что при равномерном прямолинейном движении путь равен модулю перемещения. Поэтому если нас не интересует направление движения тела, а необходимо только найти его путь, то эта формула поможет нам найти решение.

Вы смотрели Конспект по физике для 8 класса «Перемещение и описание движения».

Вернуться к Списку конспектов по физике (Оглавление).

Просмотров: 14 864

Проекция Вектора Силы своими словами для детей

Проекция вектора силы — это способ вычислить, насколько сила действует в определенном направлении.

Допустим, у тебя есть вектор силы, который показывает, как сила действует в пространстве. Но иногда нам нужно знать, как эта сила влияет на движение вдоль оси, например, вперед или назад.

Проекция вектора силы помогает нам найти эту информацию. Чтобы найти проекцию, мы берем модуль вектора (то есть его длину) и умножаем его на cosinus угла между осью и вектором.

Представь, что ты тянешь игрушечный автомобиль на ровной дороге. Сила, с которой ты тянешь его, будет вектором силы. Но ты можешь тянуть его в разных направлениях — вперед, назад, влево или вправо.

Если мы хотим узнать, насколько сила, которую ты приложил, влияет на движение автомобиля вперед, мы можем найти проекцию вектора силы на ось движения вперед.

Давай представим, что угол между осью движения вперед и вектором силы равен 30 градусам. Если модуль вектора силы равен 10 Ньютонов, то проекция будет равна 10 * cos(30) = 10 * 0.866 = 8.66 Ньютонов.

Это значит, что 8.66 Ньютонов силы будет направлено вперед и будет влиять на движение автомобиля вперед. Остальная сила будет направлена в сторону и не будет влиять на движение вперед.

Таким образом, проекция вектора силы позволяет нам разделить силу на составляющие и понять, как они влияют на движение в определенном направлении.

Относительность механического движения

Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.

Правило сложения перемещений

Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ​\( S \)​ — перемещение тела относительно неподвижной системы отсчета;
​\( S_1 \)​ — перемещение тела относительно подвижной системы отсчета;
​\( S_2 \)​ — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.

Правило сложения скоростей

Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ​\( v \)​ — скорость тела относительно неподвижной системы отсчета;
​\( v_1 \)​ — скорость тела относительно подвижной системы отсчета;
​\( v_2 \)​ — скорость подвижной системы отсчета относительно неподвижной системы отсчета.

Относительная скорость

Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное. Пусть \( v_1 \) — скорость первого тела, а \( v_2 \) — скорость второго тела.
Определим скорость первого тела относительно второго \( v_{12} \):

Пусть \( v_1 \) — скорость первого тела, а \( v_2 \) — скорость второго тела.
Определим скорость первого тела относительно второго \( v_{12} \):

Определим скорость второго тела относительно первого \( v_{21} \):

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.

Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:

Если скорости направлены под углом ​\( \alpha \)​ друг к другу, то относительная скорость рассчитывается по теореме косинусов:

Механическое движение. Система отсчёта. Закон относительности движения

Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.

То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).

Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.

Рисунок 1 – Иллюстрация к примеру

Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение

Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета

То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение

Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)

Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.

Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку. Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь

Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.

Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как  материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.

Свойства векторов

Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка. Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:

• Произведение вектора на косинус между осью и направленным отрезком равен проекции вектора.
• Проекция на ось принимает значения меньше 0, если отрезок с осью образует тупой угол.
• Проекция на ось принимает значение больше 0, если отрезок с осью образует острый угол.

Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными. Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению.

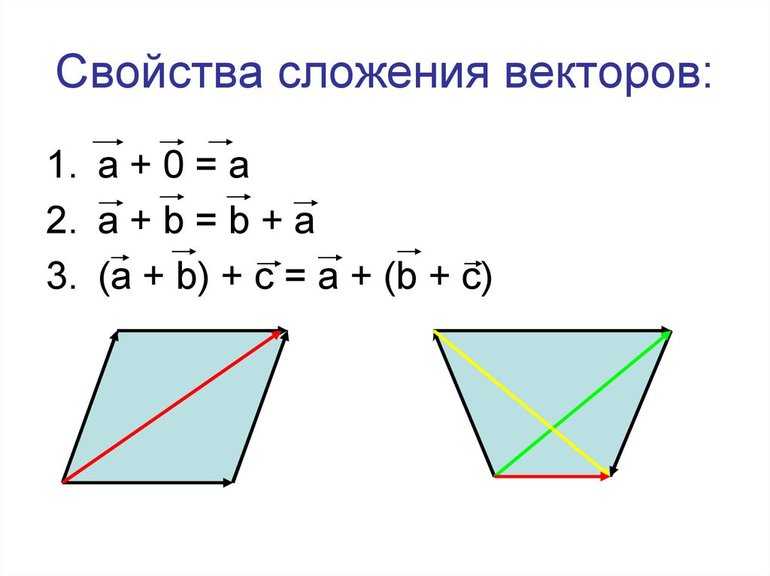
С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.

Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов.

Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов.

С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.

Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии.

Проекции вектора перемещения

При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения  (см.рис. 1.3).

Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно А_x и В_x. Длина отрезка А_xВ_x на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

Sx = AxBx

Рис. 1.3. Проекция вектора перемещения.

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть

Sx = x – x

Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:

Sy = y – y
Sz = z – z

Здесь x, y, z — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).

Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).

Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).

Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х и у, то есть А(х, у). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

Sx = x – x
Sy = y – y

На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как

АС = sx
CB = sy

По теореме Пифагора

S2 = Sx2 + Sy2

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​\( a \)​, единица измерения — м/с2.
В векторном виде:

где ​\( v \)​ – конечная скорость; ​\( v_0 \)​ – начальная скорость;
​\( t \)​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​\( a_n \)​ – нормальное ускорение, ​\( a_{\tau} \)​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если \( a_{\tau} \) ≠ 0, \( a_n \) = 0, то тело движется по прямой;
если \( a_{\tau} \) = 0, \( a_n \) = 0, ​\( v \)​ ≠ 0, то тело движется равномерно по прямой;
если \( a_{\tau} \) = 0, \( a_n \) ≠ 0, тело движется равномерно по кривой;
если \( a_{\tau} \) = 0, \( a_n \) = const, то тело движется равномерно по окружности;
если \( a_{\tau} \) ≠ 0, \( a_n \) ≠ 0, то тело движется неравномерно по окружности

Вектор перемещения

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.

Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и ), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).

Рис. 1.1. Вектор перемещения и пройденный путь.

На рис. 1.1:

Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.

Правило сложения векторов

Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).

Рис. 1.2. Сложение векторов перемещений.

На рис 1.2 показаны правила сложения векторов S1 и S2:

а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма

Значение проекций скорости в различных областях науки и техники

Физика: В физике проекции начальной скорости играют важную роль при решении задач на движение тел. Они позволяют вычислить скорость тела по осям координат и определить его траекторию. Также проекции скорости используются в уравнениях движения и законах сохранения энергии.

Авиация: В авиации проекция скорости является одним из основополагающих параметров, т.к. она позволяет контролировать скорость полета самолета, его угол наклона и направление. Например, проекции скорости используются для расчета скорости взлета и посадки, а также для поддержания оптимальной скорости во время полета на определенной высоте.

Автомобилестроение: В автомобилестроении проекции скорости также имеют большое значение. Они позволяют рассчитывать скорость автомобиля на разных участках дороги и управлять его движением. Кроме того, проекции скорости используются при тестировании автомобилей и разработке новых технологий для улучшения их управляемости.

Метеорология: В метеорологии проекции скорости используются для прогнозирования погоды и измерения скорости ветра. Например, при помощи анемометров можно измерять проекции скорости ветра на определенной высоте в атмосфере. Эта информация позволяет делать прогнозы погоды и оценивать ее влияние на различные события.

Финансы: В финансовой сфере проекции скорости также находят свое применение. Например, при анализе инвестиционных портфелей проекции скорости позволяют оценить риски, связанные с инвестированием в различные активы. Кроме того, проекции скорости используются при анализе рынка ценных бумаг и формулировании стратегии инвестирования.