Презентация на тему «история треугольника»

Содержание

Слайд 1

Слайд 2

Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых, свойства которых человек узнал еще в глубокой древности, т. к. эта фигура всегда имела широкое применение в практической жизни.
Изображения треугольников и задачи на треугольники встречаются во многих папирусах Древней Греции и Древнего Египта.. Еще в древности стали вводить некоторые знаки обозначения для геометрических фигур.

Слайд 3
Древнегреческий ученый Герон (I век) впервые применил знак вместо слова треугольник.

Слайд 4

Равносторонний треугольник символизирует завершение.
Треугольник, обращенный вершиной вверх, является солнечным и имеет символику жизни, огня.
Треугольник, обращенный вершиной вниз, является лунным и имеет символику женского начала, воды, холода.
Треугольник в круге означает мир форм, заключенный в круге вечности.
Три соединенных треугольника обозначают ненарушимое единство трех лиц Троицы.
Два смыкающихся треугольника — союз противоположностей, которые становятся жидким огнем или огненной водой.
Равносторонний треугольник свидетельствует об упрямстве, несговорчивости и методичности захвата.

Слайд 5

Благодаря знаниям свойств треугольников возникла и такая наука, как тригонометрия. Она оказалась необходимой для человека в его практических потребностях, так как ее применение просто необходимо при составлении карт, измерении участков, да и при конструировании различных механизмов.

Слайд 6
Интересные Факты:
1) В геометрии Лобачевского сумма углов треугольника всегда меньше 180. В геометрии Эвклида она всегда равна 180 . В геометрии Римана сумма углов треугольника всегда больше 180.
2) Китайцы гордятся китайским треугольником и считают, что он есть первоначалом всех фигур, и все остальные фигуры — лишь его частные случаи.
3) Первая буква большого числа алфавитов. Имеет финикийское происхождение и, чаще всего изображается в виде перевернутого треугольника.

4) Существует египетский треугольник со сторонами 3,4 и 5. Если умножить одно число на остальные два, то треугольник все равно будет египетским.

Слайд 7
Немного о Бермудском треугольнике
Бермудский треугольник является относительно недавней сенсацией. Еще на рубеже 40—50-х годов нашего столетия никому бы и в голову не пришло произнести эти два ныне магических слова, а тем более что-нибудь написать на эту тему. Настоящий взрыв раздался в 1974 году после выхода книги некоронованного короля знатоков тайн бермудского треугольника Чарльза Берлица

Сторонники Берлица ищут все новые и новые «доказательства» в пользу существования необъяснимых загадок, газеты публикуют статьи о смертельной опасности в морях треугольника, и словно голоса вопиющих в пустыне звучат немногочисленные призывы, отстаивающие серьезный подход к проблеме.

Слайд 8
СПАСИБО ЗАВНИМАНИЕ!

Посмотреть все слайды

Последние заданные вопросы в категории Геометрия

Геометрия 22.10.2023 04:51 10 Вайс Савелий

На основі АС рівнобедреного трикутника АВС позначено точки МіК такі, що АМ = CK . точка М лежить між

Ответов: 1

Геометрия 22.10.2023 04:51 14 Волкова Альфинур

Точка M середина отрезка AB. Точка N делит отрезок CD в соотношении 2:3 при отсчете от вершины C. На

Ответов: 1

Геометрия 22.10.2023 04:50 22 Скрипниченко Миша

Допоможіть, будь ласка!!! Терміново! Проходжу тест!!​

Ответов: 1

Геометрия 22.10.2023 04:50 20 Конопля Юля

помогите пожалуйста! Окружность касается сторон треугольника, длины которых равны 9, 10 и 11. Найдит

Ответов: 1

Геометрия 22.10.2023 04:50 12 Лазоренко Катя

В равнобедренном треугольнике ABC с основанием AC проведена биссектриса AD. Найдите угол 2 если угол

Ответов: 1

Геометрия 22.10.2023 04:48 8 Глухих Диана

Площини двох рівних прямокутних трапецій АВСD і КМDС взаємно перпендикулярні. Знайдіть довжину від

Ответов: 1

Геометрия 22.10.2023 04:47 20 Сабельникова София

Решите задачу по прямоугольной трапеции, найти нужно AB ОТДАЮ ВСЕ БАЛЛЫ

Ответов: 2

Геометрия 22.10.2023 04:47 16 Рябинина Мария

Длина хорды 120° центрального угла равна 6 см.Найдите длину дуги этого же угла.​

Ответов: 1

Геометрия 22.10.2023 04:46 30 Устимчук Настя

Як знайти кути рiвнобедреного трикутника.​ Якщо Зовнішній кут при основі рівнобедреного трикутника н

Ответов: 1

Геометрия 22.10.2023 04:45 29 Назарова Марина

Выыясните какие из приведённых ниже геометрических фигур могут быть проекцией прямоугольного треугол

Ответов: 1

Пример 3

Метод, известный как триангуляция, позволяет определить местоположение недоступных точек, зная другие расстояния, которые легче измерить, при условии, что сформирован треугольник, который включает желаемое местоположение между его вершинами.

Например, на следующем рисунке мы хотим знать, где находится корабль в море, обозначенный буквой B.

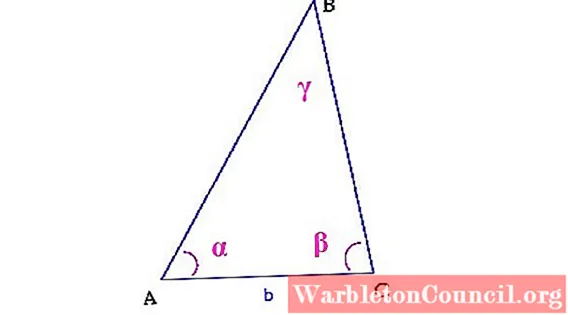
Сначала измеряется расстояние между двумя точками на берегу, которые на рисунке обозначены A и C. Затем необходимо определить углы α и β с помощьютеодолит, устройство, используемое для измерения вертикальных и горизонтальных углов.

Со всей этой информацией строится треугольник, в верхней вершине которого находится лодка. Было бы необходимо рассчитать угол γ, используя свойства треугольников и расстояния AB и CB с помощью тригонометрии, чтобы определить положение корабля в море.

Теоремы о треугольниках[]

Этот раздел не завершён.Вы поможете проекту, исправив и дополнив его.

Теорема Дезарга: если два треугольника перспективны (прямые, проходящие через соответственные вершины треугольников, пересекаются в одной точке), то их соответственные стороны пересекаются на одной прямой.

Теорема Сонда́: если два треугольника перспективны и ортологичны (перпендикуляры, опущенные из вершин одного треугольника на стороны, противоположные соответственным вершинам треугольника, и наоборот), то оба центра ортологии (точки пересечения этих перпендикуляров) и центр перспективы лежат на одной прямой, перпендикулярной оси перспективы (прямой из теоремы Дезарга).

Теорема Чевы

Теорема Менелая

История изучения понятия `треугольник` в геометрии

Треугольник — символ и важное понятие в геометрии на протяжении более чем 2,5 тысячи лет. Изображения треугольной фигуры использовались в искусстве со времен неолита, палеолита

В те времена части в рисунках использовался равносторонний треугольник. Он использовался в быту и разных сферах жизни человека: архитектуре, строительстве, во фрагментах одежды, украшениях.

Треугольник — замкнутая фигура, относящаяся к простым. Первое упоминание о нем с точки зрения математики мы встречаем в папирусах, найденных в Египте, возраст, которых превышает 4000 лет. Также первые понятия о треугольнике были приобретены людьми во времена древней Греции. Они возникли из потребности измерять площадь земельных участков, вместимость разных сосудов, предметов. Греческие ученые выстроили лаконичную систему знаний, она датируется 300 г до нашей эры и изложена в `Началах` Евклида.

В дальнейшем, для обозначения разных измерений древние люди и стали вводить специальные. Фигуру, из 3-х отрезков, 3 вершин и 3 сторон в I веке ученый Герон обозначал — V. Герон — известный ученый, инженер Древней Греции. Он продолжил исследования Евклида, Стратона, Архимеда в науке.

В современной математике простейшая фигура многоугольник с тремя вершинами и сторонами носит название треугольника или двумерного симплекса. В переводе с латыни слово `симплекс` — это простейший. Изучение свойств этой простейшей фигуры началось тоже в Древней Греции. Наиболее тщательные исследования свойств треугольника проводились в XV-XVI веках. Этими исследованиями особенно интересовался французский император Наполеон, он посещал занятия математики в свободное время. Огромный вклад в изучение фигуры треугольника и определения его свойств внес Леонард Эйлер. Закончил изучать его свойства русский ученый Лобачевский.

В процессе изучения свойств треугольника возникло несколько теорем геометрии. Самая известная из них — теорема Пифагора. Прямоугольная фигура со сторонами 3,4, 5 была известна египтянам уже с XXIII века до нашей эры. В историю она вошла как `египетский` треугольник, а еще его называли `Священным` или `Пифагоровым`.

Равенство треугольников

Случаются ситуации, когда точно известно, что два треугольника равны, а что же в таком случае можно сказать про углы и стороны таких треугольников?

Нам дано: ∆ABC = ∆A₁B₁C₁. Равны ли соответствующие стороны и углы данных фигур?

По условию треугольники равны. Значит, применяем рассмотренное правило, которое говорит о том, что все соответствующие элементы фигуры равны между собой.

Получается:

Если ∆ABC = ∆A₁B₁C_1, то равны соответствующие стороны:

АС =А₁С₁;

АВ = А₁В₁;

СВ = С₁В₁;

и соответствующие углы равны:

∠С =∠С₁;

∠А = ∠А₁;

∠В = ∠В_1.

Геометрия интересна тем, что большинство её правил нуждаются в доказательствах. Такие правила называют теоремами.

Вместе с этим, имеются и самостоятельные правила, которые называют аксиомами геометрии.

Сегодня мы рассмотрим первую теорему с названием «Первый признак равенства треугольников», и проведем работу по сбору доказательств для данной теоремы.

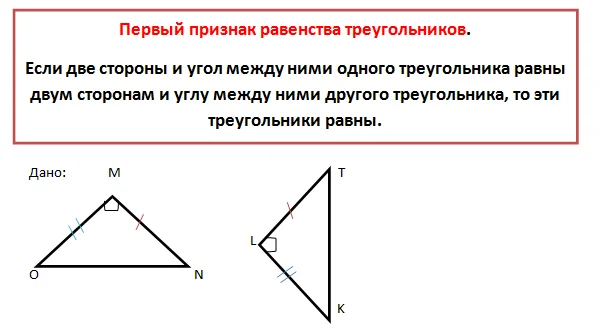
Два треугольника – ∆OMN и ∆KLT. Известно, что две стороны треугольников и угол между ними равны.

Значит:

OM=KL, 

MN=LT;

∠M =∠L.

Докажем, что ∆OMN=∆KLT.

Доказательство первого признака равенства треугольников:

Из условия нам известно, что соответствующие углы равны ∠M =∠L, следовательно, мы можем выполнить наложение двух треугольников так, чтобы вершина M совпадала с вершиной L.

Тогда, сторона OM наложится на сторону  KL, а сторона MN на отрезок LT. По условию нам известно, что отрезки равны OM=KL, MN=LT, значит, при наложении они совпадут. Получается, что при наложении совпадает угол, и две стороны, следовательно, будут совпадать и оставшиеся стороны ON и KT, то есть ON = KT . Если при наложении совмещаются три стороны и одна вершина, значит, совместятся и две другие вершины KO и TN.

Выходит, что при совмещении совпадают все элементы ∆, а такие ∆ называются равными.

Мы доказали, что ∆OMN=∆KLT.

Еще, нам предстоит познакомиться с несколькими понятиями, без которых продолжать изучение  геометрии невозможно.

Начертим прямую АВ. Выберем точку не лежащую на данной прямой. Проведем отрезок СК, соединяющий точку С и прямую АВ, таким образом, чтобы при пересечении СК и АВ образовывался прямой угол (90˚) . Изображенный отрезок СК называют перпендикуляром к прямой.

Доказательство будем проводить в два этапа.

1 этап

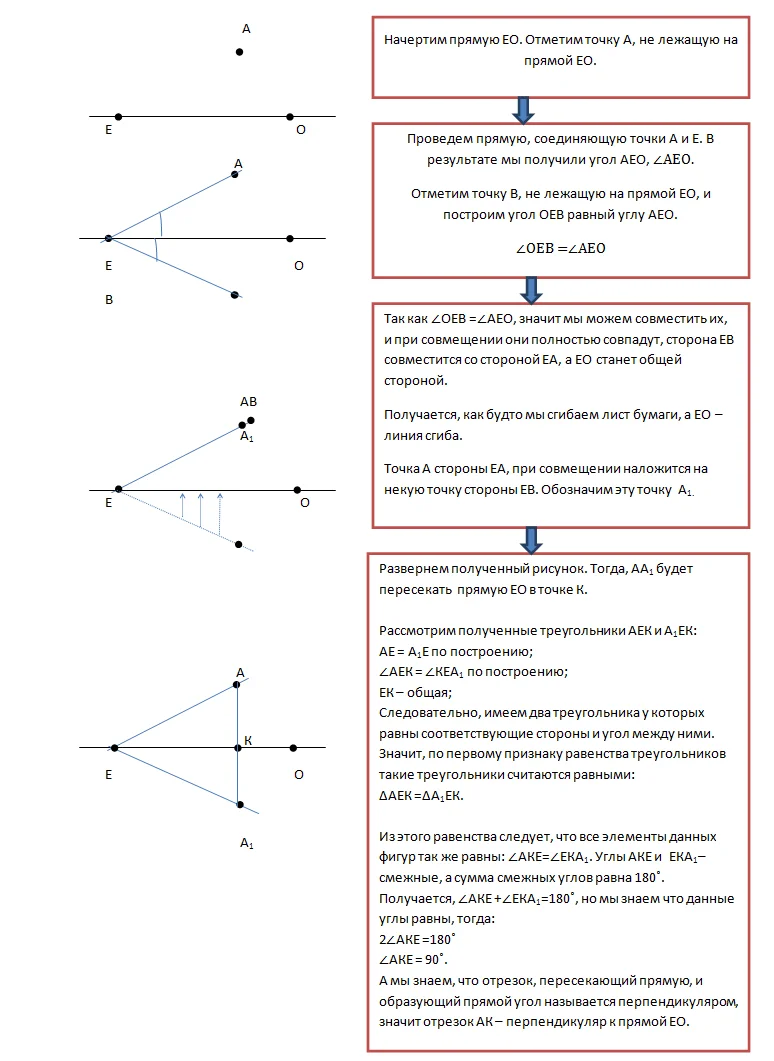2 этап

Теорема доказана.

История открытия

Паскаль ввёл в действие многие ранее недостаточно проверенные способы использования чисел треугольника, и он подробно описал их в, пожалуй, самом раннем из известных математических трактатов, специально посвящённых этому вопросу, в труде об арифметике Traité du triangle (1665). За столетия до того обсуждение чисел возникло в контексте индийских исследований комбинаторики и биномиальных чисел, а у греков были работы по «фигурным числам».

Из более поздних источников видно, что биномиальные коэффициенты и аддитивная формула для их генерации были известны ещё до II века до нашей эры по работам Пингала. К сожалению, бо́льшая часть трудов была утеряна. Варахамихира около 505 года дал чёткое описание аддитивной формулы, а более подробное объяснение того же правила было дано Халаюдхой (около 975 года). Он также объяснил неясные ссылки на Меру-прастаара, лестницы у горы Меру, дав первое сохранившееся определение расположению этих чисел, представленных в виде треугольника.

Примерно в 850 году джайнский математик Махавира вывел другую формулу для биномиальных коэффициентов, используя умножение, эквивалентное современной формуле. В 1068 году Бхаттотпала во время своей исследовательской деятельности вычислил четыре столбца первых шестнадцати строк. Он был первым признанным математиком, который уравнял аддитивные и мультипликативные формулы для этих чисел.

Примерно в то же время персидский учёный Аль-Караджи (953–1029) написал книгу (на данный момент утраченную), в которой содержалось первое описание треугольника Паскаля. Позднее работа была переписана персидским поэтом, астрономом и математиком Омаром Хайямом (1048–1131). Таким образом, в Иране фигура упоминается как треугольник Хайяма.

Известно несколько теорем, связанных с этой темой, включая биномы. Хайям использовал метод нахождения n-x корней, основанный на биномиальном разложении и, следовательно, на одноимённых коэффициентах. Треугольник был известен в Китае в начале XI века благодаря работе китайского математика Цзя Сианя (1010–1070). В XIII веке Ян Хуэй (1238–1298) представил этот способ, и поэтому в Китае он до сих пор называется треугольником Ян Хуэя.

На западе биномиальные коэффициенты были рассчитаны Жерсонидом в начале XIV века, он использовал мультипликативную формулу. Петрус Апиан (1495–1552) опубликовал полный треугольник на обложке своей книги примерно в 1527 году. Это была первая печатная версия фигуры в Европе. Майкл Стифель представил эту тему как таблицу фигурных тел в 1544 году.

В Италии паскалевский треугольник зовут другим именем, в честь итальянского алгебраиста Никколо Фонтана Тарталья (1500–1577). Вообще, современное имя фигура приобрела благодаря Пьеру Раймонду до Монтрмору (1708), который назвал треугольник «Таблица Паскаля для сочетаний» (дословно: Таблица мистера Паскаля для комбинаций) и Абрахамом Муавром (1730).

Пример 1

Говорят, что с помощью своей первой теоремы Фалес сумел измерить высоту Великой пирамиды в Египте, одного из 7 чудес древнего мира, измерив тень, которую она отбрасывает на землю, и тень, отбрасываемую колом, вбитым в землю.

Это план процедуры, которой следуют сказки:

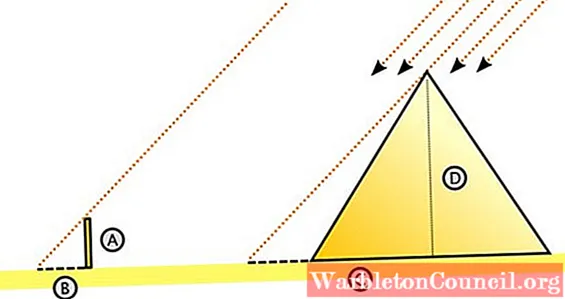
Фалес правильно предположил, что солнечные лучи падают параллельно. Имея это в виду, он представил большой прямоугольный треугольник справа.

Здесь D — высота пирамиды, а C — расстояние над землей, измеренное от центра до тени, отбрасываемой пирамидой на дно пустыни. Измерение C может быть трудоемким, но, безусловно, проще, чем измерять высоту пирамиды.

Слева находится небольшой треугольник с ножками A и B, где A — высота кола, вбитого вертикально в землю, а B — отбрасываемая им тень. Обе длины измеримы, как и C (C равно длине тени + половине длины пирамиды).

Итак, по подобию треугольников:

A / B = D / C

И высота Великой пирамиды оказывается: D = C. (A / B)

Элементы треугольника

Элементы любого треугольника указаны на следующем рисунке. Их три: вершины, стороны и углы.

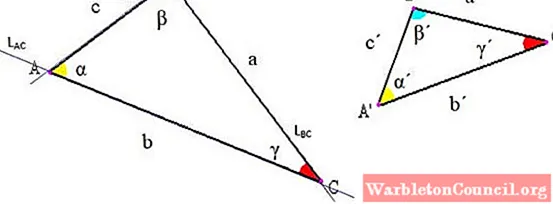
-Vertices: точки пересечения линий, отрезки которых определяют треугольник. На рисунке выше, например, линия L_AC содержащий отрезок AC, пересекает прямую L_AB который содержит отрезок AB как раз в точке A.

–Стороны: между каждой парой вершин проводится отрезок прямой, составляющий одну сторону треугольника. Этот сегмент можно обозначить конечными буквами или использовать определенную букву для его обозначения. В примере на фиг. 2 сторона AB также называется «c».

–Углы: Между каждой стороной с общей вершиной возникает угол, вершина которого совпадает с вершиной треугольника. Как правило, угол обозначается греческой буквой, как указано в начале.

Чтобы построить конкретный треугольник заданной формы и размера, достаточно иметь один из следующих наборов данных:

-Три стороны, совершенно очевидные в случае треугольника.

-Две стороны и угол между ними, и сразу прорисовывается оставшаяся сторона.

-Два (внутренних) уголка и сторона между ними. В результате прорисовываются две недостающие стороны, и треугольник готов.

Треугольник (история треугольника)

Наша Земля всегда внутри была раскаленной. Многие ее элементы, такие как газы и горные породы, стремились подняться и добраться поверхности. Самым ярким проявлением того, что под землей есть своя жизнь, стали вулканы и землетрясения.

В России хвойные места занимают очень много площади. В Российском лесе растет очень много растений. Лес является огромным подарком природы для людей. Благодаря лесу легко дышать ведь деревья выделяют кислород.

Каждый из нас любит картофельные блюда, но мало кто знает, что это растение прибыло к нам из Южной Америки. В середине 16 века эти клубни завезли в Европу. Но вначале люди не понимали всю суть употребления картофеля в пищу, и поэтому его высаживали

Треугольник является одной из первых геометрических фигур, которая стала использоваться в орнаментах древних народов. В Древнем Египте он был прямоугольным и являлся воплощением триады духовной воли, любви и высшего разума человека. Вертикальная сторона египетского треугольника составляла три единицы длины, основание— четыре, а гипотенуза — пять. Толковалась эта геометрическая фигура следующим образом: вертикальную сторону соотносили с мужским началом, основание — с женским, а гипотенуза символизировала плод их союза.

Ж.-Б. Рено. Свобода или смерть. На картине, созданной в эпоху Великой французской революции, масонский наугольник, как и фригийский колпак, является символами равенства

На Древнем Востоке почитали треугольник как символ природы всего сущего. Треугольник с вершиной, соединенной с такой же геометрической фигурой, ацтеки использовали в качестве эмблемы временного цикла. Герменевтической традиции известно множество видов треугольников, имеющих различные толкования: например, данная геометрическая фигура с горизонтальной чертой почиталась ими пассивным символом, который означает воздух, а перевернутая является олицетворением чаши, которая готова принять воду, а также соответствует женскому началу.

В Европе же данная геометрическая фигура была известна как звезда Давида. Треугольник, вписанный в окружность, олицетворяет собой мир форм, заключенный в круге вечности. Плутарх, описывая эту геометрическую фигуру, называл пространство, ограниченное сторонами треугольника, равниной истины, на которой расположены образы всего, что было и будет. Треугольники могут выступать и в качестве лунного символа, тогда они располагаются горизонтально и соприкасаются своими вершинами. Общая точка этих треугольников символически обозначает смерть и новолуние.

Магическая гексаграмма. Составляющие данную фигуру цифры не повторяются и при сочетании сумм вершин и сторон треугольника всегда дают число 26. В нумерологии целью создания подобных фигур было желание расширить и увеличить магическое воздействие цифр

В буддийской традиции два смыкающихся треугольника олицетворяют чистое пламя и Три Драгоценности Будды. Китайский символ восстановления изображается в виде треугольника с подвешенными к нему мечами, а у христиан — треугольника, образованного посредством трех пересекающихся окружностей. Это олицетворяет Троицу в единении и равенстве трех ее составляющих.

Два соединенных вершинами вертикальных треугольника разделяют символизм песочных часов, олицетворяя неумолимо идущее время и смертность. Также песочные часы часто используются для обозначения благочестивого, тихого образа жизни, краткости человеческой жизни, а также применяются как атрибут отца-времени и порой даже смерти.

Мандала Ваджраварахи. Средневековый тибетский свиток. Два наложенных друг на друга тре — уголь ника в форме гексаграммы символизируют единство мудрости и сострадания

Евклид

Евклид жил в Александрии около 300 года до нашей эры, был современником царя Птоломея I и учеником Платона. Славу Евклиду создал его собирательный труд «Начала». Произведение состояло из 13 томов, описанная в этих книгах геометрия получила название Евклидова. Величайшая заслуга его состояла в том, что он подвел итог построению геометрии придал ее изложению столь совершенную форму, что на 2 тысячи лет «Начала» стали основным руководством по геометрии.

Конечно, геометрия не может быть создана одним ученым. В работе Евклид опирался на труды десятков предшественников и дополнил работу своими открытиями и изысканиями. Сотни раз книги были переписаны от руки, а когда изобрели книгопечатание, то она много раз переиздавалась на языках всех народов и стала одной из самых распространенных книг в мире.

В одной легенде говорится, что однажды египетский царь Птолемей I спросил древнегреческого математика, нет ли более короткого пути для понимания геометрии, чем тот, который описан в его знаменитом труде, содержащемся в 13 книгах.

Ученый гордо ответил: «В геометрии нет царской дороги».

В течение многих веков «Начала» были единственной учебной книгой, по которым молодежь изучала геометрию. Были и другие. Но лучшими признавались «Начала» Евклида. И даже сейчас, в наше время, учебники написаны под большим влиянием «Начал» Евклида. (Слайд 17).

Несмотря на то, что содержание геометрии расширилось далеко за пределы учения о земле, она по-прежнему продолжает называться «Геометрией».

IV. Основные понятия планиметрии

Конечно, геометрия дает не только представление о фигурах, их свойствах, взаимном расположении, но и учит рассуждать, ставить вопросы, анализировать, делать выводы, то есть логически мыслить.

Мы начинаем изучать планиметрию.

Даже самое большое здание складывается из маленьких кирпичей, так и сложные геометрические фигуры составляются из простейших фигур.

Конечно, самая главная — это точка.

Почти все названия геометрических фигур греческого происхождения, как и само слово геометрия. Однако эти слова вошли в русский язык непосредственно не с греческого, а через латинский язык.

Точка – результат мгновенного касания, укол

Отсюда же произошел медицинский термин пункция-прокол. Пунктир.

Линия – льняная нить.

Линолеум – первоначально означал промасленное льняное полотно.

Как уже было сказано ранее, все названия геометрических фигур первоначально были названиями конкретных предметов, имеющих форму, более или менее близкую к форме данной фигуры.

V. Повторение известного материала о точках и прямых и их расположении относительно друг друга.

Давайте вспомним, как обозначают на чертеже прямые и точки.

— Прямая безгранична, поэтому на чертеже изображают часть.

— Прямые обозначают двумя заглавными латинскими буквами, соответствующим двум точкам на прямой или одной малой буквой.

— Точки обозначают заглавными латинскими буквами. (Слайд 18).

— Знак Є означает принадлежание, т.е. А Є n означает, что точка А принадлежит прямой n или лежит на ней. И C Є n соответственно, не принадлежит или не лежит. (Слайд 19).

Выполнить задание

Опишите этот рисунок, используя условные обозначения.

VI. Проверка усвоения изученного материала.

1.Практические задания № 1, 2, 3, 7.

2.Учитель выдает кроссворд каждому ученику.

Кроссворд (Слайд 20, 21).

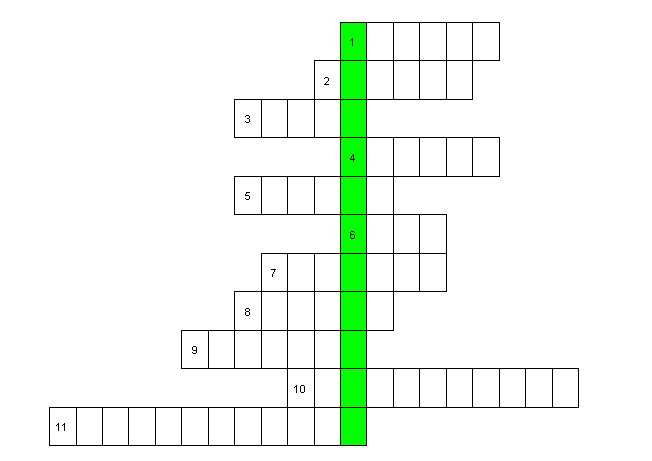
Вопросы: (Слайд 22).

1. Едет ручка вдоль листа. По линеечке, по краю. Получается черта, называется …

2. Древнегреческий ученый.

3. Результат мгновенного касания.

4.Учебная книга, состоящая из 13 томов, которая в течение многих веков являлась основным руководством по геометрии.

5. Древнегреческий ученый, автор собирательного труда «Начала».

6. Единица измерения длины.

7. Часть прямой, ограниченная двумя точками.

8. Единица измерения длины в Древнем Египте.

9. Древнегреческий математик, доказавший теорему, которая носит его имя.

10. Є математический знак.

11. Раздел геометрии.

VII. Домашнее задание № 4, 5, 6.

VIII. Подведение итогов урока.

На все ли вопросы вы получили сегодня ответы?

(Учитель обращает внимание учащихся на вопросы, поставленные в начале урока, и просит кратко еще раз на них ответить.)

Выставление отметок за практические задания и кроссворд.

Презентация к уроку: Медиа:Геометрия_вокруг_нас._Дашкина_М.Н..ppt‎

Дашкина Мариям Николаевна

Как выглядит треугольник?

В выходной день Глеб с родителями ехали в парк. Мальчик заметил, что вдоль дороги стояла непонятная табличка, увидев которую, отец поехал очень медленно.

«Что это такое?» – поинтересовался ребенок. Папа рассказал, что это дорожный знак, который предупреждает о трудностях на пути. Глебу очень понравился знак, а особенно его форма. Отец продолжил рассказ о знаках: «Форма знака о многом говорит водителю, ведь при плохой видимости автолюбитель видит только форму, а не надпись. Поэтому все предупреждающие знаки – треугольные». «А что такое треугольные?» – не унимался мальчик. Найти ответ на этот и многие другие вопросы папе помог наш сегодняшний урок.

Вначале, давайте разберемся, что же такое треугольник и из чего он состоит.

В повседневной жизни нас окружает масса предметов имеющих треугольную форму. Например:

Часы, воздушный змей, кусочек торта, пиццы, арбуза, салатники, рамки для фотографий, пузырек парфюма – этот список можно продолжать бесконечно. Но что же такое треугольник?

Приведем примеры треугольников:

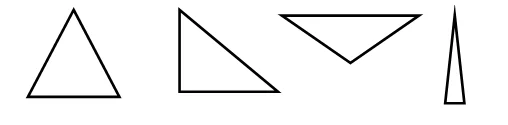
Исходя из определения, каждый рисунок состоит из трех отрезков. В геометрии такие отрезки называют сторонами треугольника.

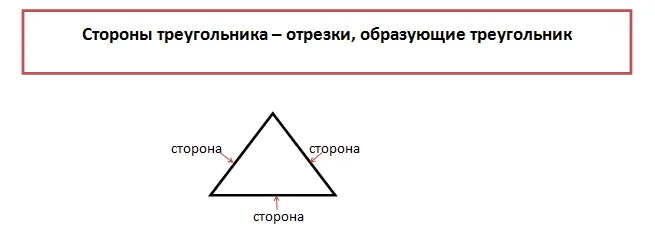
Кроме отрезков, составляющей частью фигуры являются три точки, которые принято называть вершинами.

В геометрии, вершины треугольника принято обозначать заглавными буквами латиницы: A,C,D,B.

Начертим треугольник. Вершины, обозначим буквами A,C,D.

Данная геометрическая фигура имеет три вершины A,C,D и три стороны АС, CD, DА.

А как же на письме показать, что данная фигура является треугольником?

Очень интересным является то, что записывать название, можно перечисляя вершины в любом порядке.

Например: 

Можно записать: ∆NOK, ∆OKN, ∆KNО. Каждый вариант записи обозначает один и тот же треугольник и является верным.

Само название фигуры «Треугольник» предполагает, что в состав должны входить три угла. Так ли это?

Внимательно рассмотрим рисунок:

Действительно, мы видим три угла, которые отмечены дугами: ∠RFP,∠FPR, ∠PRF(мы уже знаем, что буква, обозначающая вершину угла всегда записывается в середине) или∠F, ∠P,∠R.