Гармонические колебания

Резонанс

Резонанс – это явление, при котором система колеблется с наибольшей амплитудой при определенной частоте внешнего воздействия. В этом случае частота внешнего воздействия совпадает с собственной частотой системы, что приводит к усилению колебаний.

Резонансная частота

Резонансная частота – это частота внешнего воздействия, при которой происходит резонанс. Она определяется собственными свойствами системы и может быть вычислена с использованием уравнений колебаний.

Усиление колебаний

В резонансе колебания системы усиливаются, что приводит к увеличению амплитуды колебаний. Это происходит потому, что внешняя сила, действующая на систему, совпадает с ее собственной частотой, что приводит к синхронизации колебаний и усилению энергии системы.

Примеры резонанса

Резонанс может происходить в различных системах и имеет множество примеров в реальной жизни. Некоторые из них включают:

• Резонанс в колебаниях струн музыкальных инструментов, таких как гитара или скрипка.
• Резонанс в электрических цепях, когда частота переменного тока совпадает с резонансной частотой цепи.
• Резонанс в механических системах, таких как маятники или подвесные мосты, которые могут колебаться с большой амплитудой при определенных частотах.

Резонанс имеет важное значение в различных областях, включая физику, инженерию и музыку. Он может быть использован для усиления сигналов, определения собственных частот систем и создания эффектов в различных устройствах и технологиях

Механическая аналогия

Иногда сложно бывает понять процессы в электрических схемах, потому что все эти параметры: заряд, напряжение, ток, магнитное поле — всё же несколько абстрактны. Поэтому, мы воспользуемся аналогией с механической системой, которую легко представить и поведение которой «очевидно» из нашего жизненного опыта. А именно, рассмотрим  пружинный маятник.

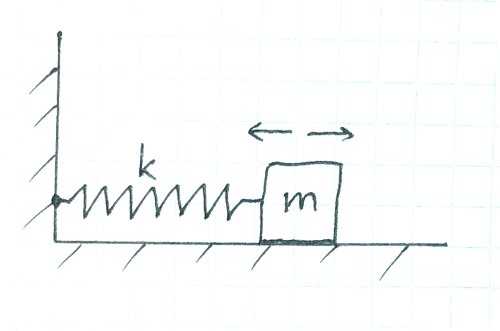
Пружинный маятник. k — коэффициент упругости пружины, m — масса грузика

Пружинный маятник представляет собой груз, закреплённый на пружине,  второй конец которой жестко зафиксирован. Груз может скользить по гладкой поверхности. Если этой системе сообщить начальную энергию (например, сжав пружину), то она начнёт совершать свободные колебания относительно точки равновесия, также описываемые гармоническим законом.

Пружина — это аналог конденсатора. Конденсатор в цепи препятствует изменению напряжения. Если попытаться повысить напряжение, то конденсатор не даст изменить его резко, скачком. Начнётся сравнительно растянутый во времени процесс заряда конденсатора. И наоборот, если внешнее напряжение падает, конденсатор будет стремиться удержать его на прежнем уровне, отдавая часть своего заряда.

Пружина тоже сопротивляется изменению своей длины. Если мы будем её сжимать или растягивать, это всегда будет сопровождаться накоплением энергии в пружине или же наоборот, высвобождением энергии (в зависимости от того, движемся ли мы к положению равновесия или от него).

Ну а грузик — это аналог катушки индуктивности. Грузик сопротивляется изменению скорости аналогично тому, как катушка индуктивности препятствует изменению тока.

В колебательной системе всегда два накопителя энергии. В нашем маятнике это потенциальная энергия сжатой пружины и кинетическая энергия грузика. Обмен энергией между ними приводит к возникновению колебаний. Чтобы окончательно убедиться в аналогии между механическими и электромагнитными колебаниями, давайте сравним формулы частоты колебаний:

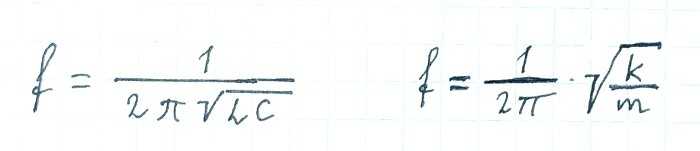
Cравнение формул частоты колебательного контура (слева) и пружинного маятника (справа)

Если принять, что 1/k — это аналог С, то, получается, формулы полностью идентичны. Остался только вопрос, почему 1/k — это аналог C. Дело в том, что чем больше ёмкость конденсатора, тем менее он «жесткий» — то есть меньше работы нужно произвести, чтобы загнать в него единицу заряда. Энергия, запасённая конденсатором, обратно пропорциональная емкости, а энергия пружины прямо пропорциональна её упругости, вот формулы:

Формула энергии заряженного конденсатора (слева) и энергии сжатой пружины (справа)

Обращаю внимание, и в том и в другом случае частота не зависит от амплитуды

Не важно, насколько большим напряжением мы зарядили конденсатор или насколько сильно сжали пружину. От количества вложенной в систему энергии будет зависеть только «размах» колебаний, амплитуда, частота же останется постоянной

От количества вложенной в систему энергии будет зависеть только «размах» колебаний, амплитуда, частота же останется постоянной.

Свободные и вынужденные колебания

Свободные и вынужденные колебания – это два основных типа колебаний, которые могут происходить в системе.

Свободные колебания

Свободные колебания – это колебания, которые происходят в системе без внешнего воздействия или воздействия внешних сил. В этом случае система имеет свою собственную частоту колебаний, которая зависит от ее свойств и начальных условий. Примером свободных колебаний может быть маятник, который колеблется взад и вперед под действием силы тяжести.

Вынужденные колебания

Вынужденные колебания – это колебания, которые возникают в системе под воздействием внешней силы или внешнего воздействия. В этом случае система колеблется с частотой, которая определяется внешней силой или воздействием. Примером вынужденных колебаний может быть колебания струны гитары под воздействием игры на ней.

Вынужденные колебания могут быть резонансными или нерезонансными. Резонансные колебания происходят, когда частота внешней силы совпадает с собственной частотой системы, что приводит к усилению колебаний. Нерезонансные колебания происходят, когда частота внешней силы не совпадает с собственной частотой системы, что приводит к ослаблению колебаний.

Свободные и вынужденные колебания имеют широкое применение в различных областях, включая физику, инженерию и музыку. Они играют важную роль в понимании и управлении колебательными системами и являются основой для различных технологий и устройств.

Гармонические колебания

Гармонические колебания – это особый тип колебаний, при которых положение объекта изменяется синусоидально во времени. Они являются наиболее простым и распространенным типом колебаний и могут быть описаны с помощью гармонической функции.

Гармоническая функция

Гармоническая функция – это математическая функция, которая описывает гармонические колебания. Она имеет вид f(t) = A * sin(ωt + φ), где:

• A – амплитуда колебаний, которая представляет максимальное отклонение объекта от его равновесного положения.
• ω – угловая частота колебаний, которая определяет скорость изменения положения объекта во времени.
• t – время, которое указывает на момент времени, в котором мы хотим узнать положение объекта.
• φ – начальная фаза колебаний, которая определяет положение объекта в начальный момент времени.

Кратко о механических колебаниях

Подробности

Обновлено 21.07.2018 11:43

Просмотров: 663

«Физика — 11 класс»

Какова общая особенность, отличающая механические колебания их от других видов механического движения?
При изучении периодических колебательных процессов особый интерес представляют общие признаки, характеризующие повторяемость в движении, а не положение и скорость колеблющегося тела в любой момент времени

Важно знать амплитуду, период и фазу колебаний, т. е

величины, характеризующие процесс в целом.
При вынужденных колебаниях надо знать отношение частоты вынуждающей силы ω и частоты свободных колебаний колебательной системы ω, т.к. именно оно определяет амплитуду и фазу колебаний.

1.
Колебания различной природы (механические, электрические и др.) описываются одинаковыми уравнениями.
Различают свободные, затухающие и вынужденные колебания.

2.
Свободные колебания возникают в системе под влиянием внутренних сил после того, как она выведена из состояния равновесия.
С течением времени свободные колебания вследствие трения затухают.

3.
Вынужденные колебания возникают при действии на систему внешней периодической силы.
Эти колебания не затухают до тех пор, пока действует внешняя сила.
Пример вынужденных колебаний: раскачивание качелей с помощью периодических толчков.

4.
Свободные колебания груза, прикрепленного к пружине, можно описать вторым законом Ньютона.
Его следствием применительно к данному случаю является уравнение

где х — смещение груза от положения равновесия; х» — ускорение груза; — постоянная, зависящая от свойств системы.

5.
Решение уравнения, описывающего свободные колебания, выражается через косинус: х = х_m cos (ωt + φ) — или синус.

Колебания, происходящие по закону косинуса или синуса, называются гармоническими.

6.
Модуль максимального смещения тела х_m от положения равновесия называется амплитудой колебаний.
Величина ω называется циклической частотой колебаний и выражается через частоту колебаний ν так:

ω = 2πν.

7.
Промежуток времени, за который система совершает одно полное колебание, называется периодом колебаний.
Период можно выразить через циклическую частоту:

8.
Величину, стоящую под знаком косинуса или синуса, называют фазой колебаний.
Фаза определяет положение колеблющегося тела в произвольный момент времени при заданной амплитуде колебаний.

9.
Собственная циклическая частота колебаний груза, прикрепленного к пружине, зависит от его массы m и жесткости пружины k:

Собственная циклическая частота колебаний математического маятника определяется формулой

где g — ускорение свободного падения,l — длина маятника.
Частота, как и период, гармонических колебаний не зависит от амплитуды.

10.
Энергия колеблющегося тела при отсутствии сил трения сохраняется:

Вынужденные колебания совершаются при воздействии на систему, в которой могут происходить колебания, периодической силы.
При этом может наблюдаться резонанс: резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы с собственной частотой колебаний системы.
Резонанс проявляется отчетливо лишь в системах с малым трением.

Следующая страница «Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии»

Назад в раздел «Физика — 11 класс, учебник Мякишев, Буховцев, Чаругин»

Механические колебания. Физика, учебник для 11 класса — Класс!ная физика

Свободные, затухающие и вынужденные колебания —
Условия возникновения свободных колебаний. Математический маятник —
Динамика колебательного движения. Уравнение движения маятника —
Гармонические колебания —
Фаза колебаний —
Превращение энергии при гармонических колебаниях —
Вынужденные колебания. Резонанс —
Примеры решения задач —
Краткие итоги главы

Основные понятия и термины

В изучении механических колебаний существуют несколько основных понятий и терминов, которые помогают нам описать и понять этот физический процесс. Рассмотрим их подробнее:

Равновесное положение

Равновесное положение – это положение объекта, в котором сумма всех действующих на него сил равна нулю. В этом положении объект не испытывает никаких внешних воздействий и остается неподвижным.

Амплитуда

Амплитуда – это максимальное отклонение объекта от его равновесного положения во время колебаний. Она характеризует величину колебаний и измеряется в единицах длины, например, в метрах.

Период

Период – это время, за которое объект выполняет одно полное колебание. Он обозначается символом T и измеряется в секундах. Период связан с частотой колебаний следующим образом: T = 1/f, где f – частота колебаний.

Частота

Частота – это количество колебаний, выполняемых объектом за единицу времени. Она обозначается символом f и измеряется в герцах (Гц). Частота связана с периодом колебаний следующим образом: f = 1/T.

Фаза

Фаза – это положение объекта во времени относительно определенной точки в колебательном процессе. Она измеряется в радианах или градусах. Фаза определяет, насколько объект отстает или опережает свое равновесное положение.

Фазовая разность

Фазовая разность – это разница в фазе между двумя колеблющимися объектами. Она измеряется в радианах или градусах и показывает, насколько один объект отстает или опережает другой в колебательном процессе.

Демпфированные колебания

Демпфированные колебания – это колебания, в которых энергия системы постепенно теряется из-за сил трения или сопротивления среды. При демпфированных колебаниях амплитуда постепенно уменьшается со временем.

Свободные и вынужденные колебания

Свободные колебания – это колебания, которые происходят без внешнего воздействия или воздействия внешних сил. Они возникают, когда система имеет начальное отклонение от равновесного положения и начинает колебаться самостоятельно.

Вынужденные колебания – это колебания, которые возникают под воздействием внешних сил или внешнего источника энергии. Внешние силы могут вызывать колебания с определенной частотой и амплитудой.

Резонанс

Резонанс – это явление, при котором система колеблется с наибольшей амплитудой при определенной частоте внешнего воздействия. Резонанс может быть полезным, например, в музыкальных инструментах, или нежелательным, когда вызывает разрушительные последствия, например, в зданиях или мостах.

Эти основные понятия и термины помогают нам описать и понять различные аспекты механических колебаний. Их понимание является важным для изучения и применения колебательных процессов в различных областях науки и техники.

Применение колебательного контура

Собственная частота колебательного контура одновременно является и резонансной частотой. На резонансной частоте общее сопротивление параллельного колебательного контура является максимальным. Поэтому его используют как элемент фильтров: когда из сложного сигнала с запутанным спектром нужно выделить узкий диапазон частот. Колебательный контур как раз и выделяет частоты, близкие к резонансной, заметно ослабляя более низкие (закорачивая их через низкое реактивное сопротивление катушки) или более высокие частоты (они уходят через низкое сопротивление конденсатора).

К примеру, колебательный контур часто располагают на входе радиоприёмника: он позволяет выделять из всего спектра радиочастот сигнал только одной радиостанции. Причём этот контур можно сделать  перестраиваемым, заменив постоянный конденсатор на подстроечный, ёмкость которого можно менять поворотом ручки. Так что приёмник сможет настраиваться на разные радиостанции.

Также колебательный контур может быть элементом генератора, задавая его рабочую частоту. Нужно только сделать положительную обратную связь: усилить сигнал, полученный от контура, а затем часть этого усиленного сигнала вернуть обратно в контур, компенсируя таким образом все возможные потери и делая колебания незатухающими.

Собственная частота колебательного контура

Какова будет частота этих колебаний? Она зависит от параметров конденсатора и катушки индуктивности, и вычисляется по формуле Томсона:

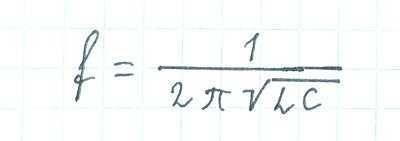
Формула Томпсона для расчёта частоты колебательного контура. L — индуктивность катушки (Гн), C — ёмкость конденсатора (Ф)

Чем больше ёмкость и индуктивность, тем медленнее конденсатор и катушка накапливают и отдают энергию, и тем ниже будет частота.

Также следует отметить, что на резонансной частоте реактивные сопротивления катушки и конденсатора равны. То есть частота собственных колебаний автоматически устанавливается такой, чтобы катушка и конденсатор получали одинаковые порции энергии.

Демпфированные колебания

Демпфированные колебания – это тип колебаний, при которых энергия системы с течением времени уменьшается из-за наличия силы трения или сопротивления. Эта сила противодействует движению объекта и приводит к затуханию колебаний.

Существует три основных типа демпфированных колебаний:

Перекрестные колебания

Перекрестные колебания происходят, когда сила трения или сопротивления прямо пропорциональна скорости движения объекта. Это означает, что чем быстрее движется объект, тем больше сила трения или сопротивления действует на него. При этом колебания затухают со временем и объект возвращается к своему равновесному положению.

Критические колебания

Критические колебания происходят, когда сила трения или сопротивления равна силе восстанавливающей силы, которая стремится вернуть объект к его равновесному положению. В этом случае колебания затухают максимально быстро и объект также возвращается к своему равновесному положению.

Перекрестные колебания

Перекрестные колебания происходят, когда сила трения или сопротивления обратно пропорциональна скорости движения объекта. Это означает, что чем медленнее движется объект, тем больше сила трения или сопротивления действует на него. В этом случае колебания затухают со временем, но объект может не достичь своего равновесного положения и остановиться в некотором отклоненном положении.

Демпфированные колебания широко применяются в различных областях, включая механику, электронику и акустику. Они играют важную роль в управлении и контроле колебательных систем, а также в создании амортизационных устройств для снижения вибраций и шума.

Понимание колебаний

Колебания увлекательное явление что можно наблюдать в различные системы, Из механические системы в электрические цепи. Они включают в себя повторяющиеся возвратно-поступательные движения объекта или системы вокруг центральное положение. В более простые термины, колебания относятся к регулярное качание или вибрационное движение объекта.

Определение колебаний

Колебания можно определить как что собой представляет периодическое движение объекта или системы между две крайние точки или должности. Это движение характеризуется наличием отдыхсила сжатия это приносит объект вернуться в свое равновесное положение. Восстанавливающая сила действует в противоположное направление к смещению объект, заставляя его колебаться вокруг точка равновесия.

In контекст колебаний, несколько ключевых терминов важно понимать:

1. Амплитуда: Максимальное смещение of колеблющийся объект от своего положения равновесия.
2. Периодическая сила: Внешняя сила которое периодически применяется к колебательной системе, заставляя ее колебаться.
3. Восстановление силы: Сила который действует на объект или систему, возвращая его в положение равновесия.
4. Частота колебаний: Номер of полные колебания или циклы, которые происходят в определенный период времени.
5. Период колебаний: Время взято за одно полное колебание или цикл, чтобы произойти.
6. Разность фаз: Разница в фазе между два колеблющихся объекта или системы.
7. Демпфирующая сила: Сила который противодействует движению колеблющийся объект, что приводит к рассеиванию энергии и уменьшение по амплитуде.
8. Коэффициент демпфирования: Измерять of демпфирование Сила в колебательной системе.
9. Коэффициент демпфирования: Соотношение of фактическое демпфирование коэффициент в критический коэффициент демпфирования.
10. Критическое демпфирование: Условия демпфирования, при которых колебательная система возвращается в положение равновесия без любое колебание.
11. Недостаточное демпфирование: Условия демпфирования, при которых колебательная система испытывает колебания, которые постепенно уменьшаются по амплитуде.
12. Передемпфирование: Условия демпфирования, при которых колебательная система возвращается в свое положение равновесия без колебаний, но с более медленная скорость конвергенции.
13. Переходное состояние: Начальная фаза of колебание в котором поведение системы находится под влиянием его первоначальные условия.
14. Устойчивое колебание: Долгосрочное поведение колебательной системы после переходное состояние прошел.
15. Собственная частота: Частота, с которой колебательная система имеет тенденцию колебаться в отсутствие какой-либо внешней силы.
16. Резонанс: Феномен где колебательная система вынуждена колебаться на своей собственная частота внешней силой.
17. Резонансная частота: Частота какой резонанс происходит в колебательной системе.
18. Гармонический генератор: Система который демонстрирует простые гармонические колебания, где возвращающая сила прямо пропорциональна смещению.

Типы колебаний

Колебания можно разделить на Различные типы на основе различных факторов. Некоторые распространенные типы колебаний включают в себя:

1. Свободное колебание: Также известен как естественное или невынужденное колебаниеЭто происходит, когда колебательная система может колебаться сама по себе без какой-либо внешней силы.
2. Управляемое колебание: Этот тип Колебания возникают, когда к колебательной системе постоянно прикладывается внешняя сила, заставляющая ее колебаться с частотой, отличной от ее собственная частота.
3. Принудительная вибрация: Когда на колебательную систему действует внешняя сила, соответствующая ее собственная частота, он подвергается вынужденная вибрация, В результате чего колебания большой амплитуды.
4. Механический резонанс: Феномен где колебательная система колеблется с максимальная амплитуда на его собственная частота из-за эффект резонанса.
5. Система колебаний: Система совершающее колебательное движение, например маятник, система масса-пружина или электрическая LC-цепь.

Понимание колебаний имеет решающее значение в различных областях, включая физику, инженерию и даже музыка. Изучая поведение колебательные системы, мы можем получить представление о основополагающие принципы управляющие движением объектов и систем в наш мир.

Звук

Звук – это колебания упругой среды, воспринимаемые органом слуха.

Условия, необходимые для возникновения и ощущения звука:

• наличие источника звука;
• наличие упругой среды между источником и приемником звука;
• наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
• мощность звука должна быть достаточной для восприятия.

Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.

Классификация звуковых волн:

• инфразвук (​\( \nu \)​ < 16 Гц);
• звуковой диапазон (16 Гц < \( \nu \) < 20 000 Гц);
• ультразвук (\( \nu \) > 20 000 Гц).

Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.

Скорость звука зависит

от упругих свойств среды:

в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;

от температуры среды:

в воздухе при температуре 0°С – 331 м/с,
в воздухе при температуре +15°С – 340 м/с.

Характеристики звуковой волны

• Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
• Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
• Тембр – это окраска звука.

Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны.Шум – хаотическая смесь тонов.

Амплитуда, период и частота колебаний

Амплитуда колебаний (A) – это максимальное отклонение объекта от его равновесного положения. Она характеризует величину колебаний.

Период колебаний (T) – это время, за которое объект выполняет одно полное колебание. Он обратно пропорционален частоте колебаний и может быть выражен как T = 1/f, где f – частота колебаний.

Частота колебаний (f) – это количество колебаний, выполняемых объектом за единицу времени. Она обратно пропорциональна периоду колебаний и может быть выражена как f = 1/T.

Амплитуда, период и частота колебаний являются основными характеристиками гармонических колебаний и позволяют нам описывать и анализировать их свойства.

Амплитуда определяет максимальное отклонение объекта от его равновесного положения. Например, если мы рассматриваем колебания маятника, то амплитуда будет определять максимальный угол отклонения маятника от вертикального положения.

Период колебаний – это время, за которое объект выполняет одно полное колебание. Например, если мы рассматриваем колебания маятника, то период будет определять время, за которое маятник совершает полный цикл отклонения в одну сторону и обратно.

Частота колебаний – это количество колебаний, выполняемых объектом за единицу времени. Она обратно пропорциональна периоду колебаний и может быть выражена как f = 1/T. Например, если период колебаний маятника составляет 2 секунды, то частота колебаний будет равна 1/2 = 0.5 Гц, что означает, что маятник совершает полное колебание в одну сторону и обратно каждые 2 секунды.

Амплитуда, период и частота колебаний являются важными параметрами, которые позволяют нам описывать и анализировать колебательные системы. Они также связаны между собой и изменение одного из них может влиять на другие параметры колебаний.

Примеры механических колебаний

Маятник

Маятник – это простой пример механических колебаний. Он состоит из точечной массы, подвешенной на невесомой нити или стержне. Когда маятник отклоняется от равновесия и отпускается, он начинает колебаться вокруг своей равновесной позиции. Маятник может быть математически описан гармоническими колебаниями, где его период зависит от длины нити и ускорения свободного падения.

Колебания пружины

Колебания пружины – это еще один пример механических колебаний. Пружина закреплена на одном конце и имеет точечную массу на другом конце. Когда масса отклоняется от равновесия и отпускается, пружина начинает колебаться вокруг своей равновесной позиции. Колебания пружины также могут быть описаны гармоническими колебаниями, где период зависит от массы и жесткости пружины.

Звуковые волны

Звуковые волны – это механические колебания, которые распространяются через среду, такую как воздух или вода. Когда источник звука, такой как колеблющаяся струна или вибрирующая мембрана, создает колебания, они передаются через среду в виде звуковых волн. Звуковые волны могут быть описаны различными параметрами, такими как амплитуда (громкость), частота (высота звука) и длина волны.

Сейсмические волны

Сейсмические волны – это колебания, которые возникают в земле в результате землетрясений или других геологических процессов. Сейсмические волны могут быть разных типов, включая продольные (P-волны) и поперечные (S-волны). Они распространяются через землю и могут быть зарегистрированы сейсмографами. Изучение сейсмических волн позволяет ученым изучать внутреннюю структуру Земли и предсказывать возможные опасности.

Волны на водной поверхности

Волны на водной поверхности – это колебания, которые возникают в воде под воздействием ветра, гравитации или других факторов. Волны могут быть разных типов, включая поверхностные волны, такие как волны в океане или на озере, и внутренние волны, которые возникают в границе раздела двух слоев воды разной плотности. Волны на водной поверхности имеют свои характеристики, такие как амплитуда, длина волны и период, и они играют важную роль в океанографии и судоходстве.