Что представляет собой нитяной маятник кратко

Интересные факты о нитяных маятниках

Нитяной маятник – это физическое устройство, которое представляет собой подвесной механизм с грузом на конце нити. Он используется для исследования различных физических явлений, включая гравитацию, инерцию и движение.

Вот несколько интересных фактов о нитяных маятниках:

• Опыты с нитяными маятниками были проведены еще в XVII веке. Один из самых известных ученых, кто изучал маятники, был французский физик Жан-Бернар Леон Фукуо (коротко Леонардо да Винчи).
• Нитяной маятник используется для измерения времени. Период колебаний маятника является регулярным и зависит только от длины его нити и гравитационного поля Земли.
• Маятники могут использоваться для определения широты. На экваторе маятник будет двигаться в горизонтальной плоскости, а на полюсе – в вертикальной плоскости. В остальных широтах он будет двигаться под углом к горизонту.
• Нитяные маятники используются в художественных инсталляциях. Их грациозные движения и непредсказуемое поведение делают их популярным элементом визуального искусства.

Нитяные маятники – довольно удивительные устройства, которые могут открывать новые знания о мире вокруг нас. Они продолжают удивлять и вдохновлять людей своими движениями и простотой в использовании.

Математическое обоснование

Нитяной маятник – это простой механический система, состоящая из нити и точечной массы, подвешенной на нити. Нитяной маятник представляет собой один из наиболее изученных объектов в физике и математике.

Определим основные физические характеристики нитяного маятника:

• Длина нити (L) — расстояние от точки подвеса до центра масс;
• Масса точечной массы (m) — количество вещества, которое содержится в точечной массе;
• Ускорение свободного падения (g) — ускорение, с которым тело падает в поле тяжести;
• Угол отклонения (θ) — угол между положением равновесия (прямое вертикальное положение) и текущим положением маятника.

Математическое обоснование движения нитяного маятника основывается на законе Гука для вращательного движения. Этот закон позволяет связать период колебаний маятника с его характеристиками.

1. Период колебаний нитяного маятника (T) можно выразить следующей формулой:

T = 2π√(L/g)

Где π (пи) — математическая константа, равная приблизительно 3.14159.

Амплитуда колебаний (A) маятника зависит от начального отклонения и определяется следующей формулой:

A = L * sin(θ)

Математическое обоснование позволяет предсказывать и описывать движение нитяного маятника с помощью физических и геометрических закономерностей. Это позволяет использовать нитяной маятник в различных областях науки, техники и технологий.

Точность измерений

Нитяной маятник — это физическая система, используемая для измерения времени в различных научных и технических областях. Он представляет собой маятник, свисающий на нити и осуществляющий колебания под воздействием гравитационных сил.

Измерение времени с помощью нитяного маятника основано на математической формуле, известной как формула периода колебаний. Согласно этой формуле, период колебаний (время, за которое маятник проходит полный цикл) зависит от длины нити и ускорения свободного падения.

Точность измерений нитяного маятника определяется различными факторами. Одним из них является точность измерения длины нити, которая должна быть измерена с высокой точностью, чтобы минимизировать ошибку в результате. Другим фактором является стабильность условий эксперимента, таких как температура и воздушное сопротивление, которые могут влиять на колебания маятника.

Для повышения точности измерений нитяного маятника могут использоваться различные методы и техники. Например, можно провести несколько измерений и усреднить полученные результаты для уменьшения случайной ошибки. Также можно использовать более точные инструменты для измерения длины нити и ускорения свободного падения.

• Для увеличения точности измерений нитяного маятника:
• Используйте более точные инструменты для измерения длины нити и ускорения свободного падения.
• Проведите несколько измерений и усредните полученные результаты.
• Обеспечьте стабильные условия эксперимента, контролируя температуру и воздушное сопротивление.

Точность измерений нитяного маятника играет важную роль во многих научных и технических областях, таких как астрономия, физика и инженерия. Она позволяет вести точные измерения времени, что имеет значение для решения различных задач и испытаний.

Нитяной и пружинный маятники

Познакомимся с физической моделью нитяной маятник. Взгляните на рисунок. Вы видите кирпич, подвешенный на широкой ленте, и тяжёлый шарик, подвешенный на нити. Толкнём их рукой, и оба тела начнут совершать колебания – станут маятниками.

Изучить колебания – значит найти способы описания колебаний и выявить их закономерности. Удобен ли для этого кирпичный маятник? Конечно, нет. Во-первых, потому, что он большой, и при его качаниях будет велика сила сопротивления воздуха. Во-вторых, лента подвешена за два конца, и при качаниях её половины будут натягиваться неодинаково, из-за чего кирпич будет двигаться зигзагами. Тяжёлый шарик на нити более удобен для изучения колебаний.

Нитяным маятником называют тело на невесомой нерастяжимой нити, совершающее колебания

Для этой модели важно, чтобы размеры тела были малы по сравнению с длиной нити

В таком случае говорят: формой и размерами тела можно пренебречь (то есть в данных условиях не принимать их во внимание)

Опыты показывают: если на тело нитяного маятника действуют только сила тяжести и сила упругости, он совершает колебания с постоянным периодом. При этом, если амплитуда колебаний невелика по сравнению с длиной нити (говорят: маятник совершает малые колебания), то период колебаний нитяного маятника можно подсчитать по формуле, которая помещена в рамке.

Вы видите, что период малых колебаний нитяного маятника не зависит от его массы, а определяется лишь длиной нити l и коэффициентом g. Например, при увеличении длины нити в 4 раза, период колебаний маятника возрастёт в 2 раза (что равно √4 раз).

Рассмотрим вторую модель: пружинный маятник – тело на пружине, совершающее колебания

При этом важно, чтобы один конец пружины был закреплён, а её масса была мала по сравнению с массой тела (то есть массой пружины можно было бы пренебречь)

Опыты показывают: если на тело пружинного маятника действуют только сила тяжести и сила упругости, он совершает колебания с постоянным периодом. При этом, если амплитуда колебаний невелика по сравнению с длиной пружины (то есть она деформируется упруго), то период колебаний пружинного маятника можно подсчитать по формуле, которая помещена в рамке.

Итак, период малых колебаний пружинного маятника не зависит от коэффициента силы тяжести, а определяется лишь массой тела m и коэффициентом k, характеризующим жёсткость пружины. Например, при увеличении массы груза в 9 раз, период колебаний маятника возрастёт в 3 раза (что равно √9 раз).

Наряду со свободными колебаниями, когда маятник выведен из положения равновесия и предоставлен самому себе, существуют также вынужденные колебания и автоколебания. Обратимся к рисунку. Под гирей, висящей на пружине, расположен электромагнит. Если мы будем попеременно включать и выключать ток, то гиря начнёт совершать вынужденные колебания, частота которых зависит от частоты внешнего воздействия.

Однако маятник может сам регулировать поступление энергии, совершая автоколебания. Взгляните: средний провод зажат прищепкой и касается гири, пока она вверху. Ток, проходя через пружину, гирю, средний провод и электромагнит, намагничивает его сердечник. Притягиваясь, гиря движется вниз. Вскоре она отсоединяется от среднего провода, ток прекращается, и магнитное поле исчезает. Под действием пружины гиря поднимается вверх и снова замыкает цепь.

Преимущества нитяного маятника

Нитяные маятники, благодаря своей конструкции и основным принципам работы, обладают несколькими важными преимуществами:

1. Высокая точность измерений	Нитяные маятники используются во многих научных и технических приборах, где требуется высокая точность измерений. Благодаря постоянству периода колебаний и малому влиянию внешних факторов, нитяные маятники обладают способностью измерять время с высокой точностью.
2. Простота устройства	Устройство нитяного маятника довольно просто, что позволяет легко изготавливать и поддерживать его. Кроме того, простота конструкции позволяет упрощать анализ и использование нитяного маятника как модели для изучения различных физических явлений.
3. Устойчивость	Нитяные маятники обладают высокой устойчивостью к внешним воздействиям, таким как температурные колебания, вибрации и электромагнитные поля. Это делает их надежными и подходящими для использования в различных условиях.
4. Экономическая эффективность	Нитяные маятники являются относительно недорогими в изготовлении и эксплуатации. Их простота и доступность материалов позволяют использовать их в различных областях, не требуя значительных затрат.

Все вышеперечисленные преимущества делают нитяные маятники важным инструментом для научных исследований, технических приложений и образования, а также способствуют развитию физики и других наук.

Топ вопросов за вчера в категории Физика

Физика 19.06.2023 23:44 3090 Трухман Дарья

6. По графику зависимости скорости равномерно дви- жущегося тела от времени (рис. 43) определите с

Ответов: 1

Физика 28.09.2023 20:06 4828 Копылова Алёна

3) Предложите единицы скорости, не указанные в параграфе.7 класс Физика​

Ответов: 2

Физика 05.06.2023 05:32 1966 Блок Богдана

7. По графикам зависимости пути от времени (рис. 44) двух тел, движущихся равномерно, определите,

Ответов: 1

Физика 20.06.2023 14:02 3482 Ашкенова Дарига

Скоростной поезд за 10 минут проходит путь, равны 40 км. Определить его среднюю скорость.

Ответов: 1

Физика 29.04.2023 12:23 4789 Парамонов Александр

К неподвижном у телу массой 20 кг приложили постоянную силу 6Н .Какую скорость приобретёт тело за15с

Ответов: 2

Физика 08.11.2018 21:44 185 Вологдина Лиза

ФИЗИКА!!потенциальная энергия взаимодействия с землей гири массой 5 кг увеличилась на 75 дж.На сколь

Ответов: 1

Физика 20.06.2023 01:53 1247 Милованова Виктория

постройте графики зависимости пути от времени для тел, одно из которых движется с постоянной скорост

Ответов: 1

Физика 09.01.2020 05:53 2468 Хлыбов Глеб

С какой скоростью плывет лосось, если за 5 секунд он проплыл 30 метров

Ответов: 2

Физика 03.06.2023 02:50 505 Земляной Дима

Первую половину пути из Москвы в Подольск автомобиль ехал со скоростью 90 км ч а оставшийся путь 20

Ответов: 2

Физика 21.06.2023 05:58 2119 Кулик Станислав

при полном сгорании 6кг топлива выделилось количество теплоты 2,76*10 в 8 степени. О каком топливе и

Ответов: 1

Величины, характеризующие колебательное движение

Ранее рассматривались такие характеристики колебаний, как период, частота и амплитуда. Помимо этих величин, колебания характеризуются фазой колебаний.

Фаза колебаний

На рисунке 7 изображен график зависимости смещения от времени при гармонических колебаниях. Такой график называется синусоидой (косинусоидой). В общем случае уравнение зависимости координаты Х от времени t будет выглядеть так:

Разность фаз

Понятие «разность фаз» применяется, когда мы хотим сравнить движение двух маятников. Пусть маятник 1 и маятник 2 двигаются по законам соответственно:

Найдем разность фаз колебаний этих двух маятников.

— это начальные фазы колебания первого и второго маятников соответственно. Эти величины являются начальными условиями, и они не изменяются во время движения, следовательно, при одинаковой частоте колебаний маятников разность фаз остается постоянной.

Последние заданные вопросы в категории Физика

Физика 22.10.2023 07:53 5 Естафьева Соня

1. (а) Окушы удемелi козгалган автомобильдiн әртүрлi орын ауыстыруы кезiндегi сонгы жылдамдыгын елше

Ответов: 1

Физика 22.10.2023 07:49 21 Иванов Георгий

ДАМ 50 БАЛОВ ПЖпжпжпж​

Ответов: 1

Физика 22.10.2023 07:48 29 Сейсенбай Жасулан

До атома Оксигену приєднався один електрон. При цьому утворився позитивний чи негативний йон?

Ответов: 1

Физика 22.10.2023 07:48 2 Тефтеров Денис

Допоможіть будь ласка дуже потрібно((((( Є прилад з ціною поділки 1 мкА і кількістю поділок 100. В

Ответов: 1

Физика 22.10.2023 07:47 9 Катахова Люба

R=800 м V = 20 м/с Q-?

Ответов: 1

Физика 22.10.2023 07:47 8 Серикжанулы Жансерик

6. Третину часу потяг рухався зі швидкістю 80 км/год, наступну третину часу — зі швидкістю 62 км/год

Ответов: 2

Физика 22.10.2023 07:47 18 Жалин Вадим

Брусок з заліза має масу в 6 кг , щоб утримати його у воді потрібно прикласти силу 60H Яка сила архі

Ответов: 0

Физика 22.10.2023 07:47 5 Смирнов Евгений

Терміново! Даю 50 балів Задача 1. Рівнянням = 2 − 3^2 + 4^3 (м) дана залежність шляху, пройденого

Ответов: 2

Физика 22.10.2023 07:45 8 Rakhimov Azat

Лабораторна робота 1 фізика 7 клас

Ответов: 1

Физика 22.10.2023 07:43 14 Юлташев Рамиль

Кинуте під кутом 30° до горизонту тіло перебувало в русі рівно дві секунди. Чому буде дорівнювати ма

Ответов: 1

Период колебаний математического маятника

Выведем формулу периода колебаний нитяного маятника взяв за идеальную модель математический маятник.

Если масса маятника длиной $l$ описывает колебания по дуге с углом отклонения $α$, то проекция силы тяжести на касательную к траектории (именно по этой касательной направлена мгновенная скорость маятника) равна:

$$F=-mgsin\alpha$$

По второму закону Ньютона проекция ускорения на касательную к траектории маятника :

$$a_т={F\over m}$$

Подставив эту формулу в предыдущую, и сократив массу, получаем:

$$a_т=-gsin\alpha$$

Учитывая, что для малых углов $sin\alpha=\alpha$ и отклонение маятника $s=\alpha l$, можно записать:

$$a_т=-{g\over {l}}s$$

Ускорение – это вторая производная перемещения. В вышей математике доказывается, что единственная функция, вторая производная которой пропорциональна самой себе со знаком минус – это круговая функция. Решением данного уравнения является функция:

$$s(t)=S_{max} cos \sqrt{g\over l}t$$

Рис. 2. График колебаний математического маятника.

Периодом этой функции будет величина:

$$T=2\pi\sqrt {l\over g}$$

Данная формула была установлена Х. Гюйгенсом.

Если обратиться к формулам движения и периода колебаний пружинного маятника, можно видеть, что эти формулы почти одинаковы. Жесткости пружины в пружинном маятнике соответствует ускорение свободного падения в математическом маятнике. Длине математического маятника соответствует масса груза в пружинном маятнике. Это говорит о том, что в обоих случаях колебательные процессы имеют один и тот же механизм возникновения – сила, двигающая груз, зависит от отклонения, и направлена всегда против этого отклонения.

Колебания

Формула периода колебания математического маятника впервые была открыта голландским ученым Гюйгенсом в далеком XVII веке. Будучи современником Исаака Ньютона, Гюйгенс был очень увлечен такими вот маятниками, увлечен настолько, что даже изобрел специальные часы с маятниковым механизмам, и часы эти были одними из самых точных для того времени.

Маятниковые часы Гюйгенса.

Появление подобного изобретения сослужило большую пользу физике, особенно в сфере физических экспериментов, где точное измерение времени является весьма важным фактором.

Но вернемся к маятнику, итак, в основе работы маятника лежат его колебания, которые можно выразить формулой, точнее следующим дифференциальным уравнением:

x + w2 sin x = 0

Где х (t) – неизвестная функция (это угол отклонения от нижнего положения равновесия в момент t, выраженный в радианах); w – положительная константа, которая определяется из параметров маятника (w = √ g/L, где g – это ускорение свободного падения, а L – длина математического маятника (подвес).

Помимо, собственно колебаний маятник может пребывать и в положении равновесия, при этом сила тяжести, действующая на него, будет уравновешиваться силой натяжения нити. Обычный плоский маятник, пребывающий на нерастяжимой нити, является системой с двумя степенями свободы. Но если, к примеру, нитку заменить на стержень, тогда наш маятник станет системой лишь с одной степенью свободы, так как его движения будут двухмерными, а не трехмерными.

Но если же наш маятник все-таки пребывает на нити и при этом совершает интенсивные колебания вверх-вниз, тогда механическая система приобретает устойчивое положение, именуемое «верх тормашками», еще ее называют маятником Капицы.

Свойства

У маятника есть ряд интересных свойств, подтвержденных физическими законами. Так период колебаний всякого маятника зависит от таких факторов, как его размер, форма тела, расстояние между центром тяжести и точкой подвеса. Поэтому определение периода маятника является не простой задачей. А вот период математического маятника можно рассчитать точно по формуле, которая будет приведена ниже.

В ходе наблюдений за маятниками были выведены следующие закономерности:

• Если к маятнику подвешивать разные грузы с разным весом, но при этом сохранять одинаковую длину маятника, то период его колебания будет одинаковым вне зависимости от массы груза.
• Если при запуске колебаний отклонить маятник на не очень большие, но все же разные углы, то он станет колебаться в одинаковым период, но по разным амплитудам. Следовательно, период колебания у подобного маятника не зависит от амплитуды колебания, такое явление было названо изохронизмом, что с древнегреческого можно перевести как «хронос» – время, «изо» – равный, то есть «равновременный».

Применение нитяного маятника

1. Физика и наука

Нитяной маятник используется в физических экспериментах для определения коэффициента трения и других физических параметров. Он также является инструментом для изучения гравитационных и механических свойств материалов.

2. Геополитика

В геополитических и геофизических исследованиях, нитяной маятник используется для изучения внутренних слоев Земли. Он помогает узнать о гравитационном поле Земли, скорости земных волн и других параметров, которые могут помочь улучшить наши знания о структуре планеты.

3. Медицина

В медицине, нитяной маятник используется для измерения пульса пациента и для определения состояния нервной системы. Он также может быть использован для оценки реакции на стимуляцию, такую как звуковые волны. В некоторых случаях, нитяной маятник может использоваться как инструмент для положительной терапии.

4. Динамические исследования

Как масса влияет на поведение нитяного маятника

Когда масса нити и точки подвеса маятника пренебрежимо мала по сравнению с массой маятника, такой маятник считается математическим. Такое упрощение позволяет использовать законы физики и математические модели для описания и предсказания поведения маятника.

Чем больше масса маятника, тем больше сила гравитации, действующая на него. Это может привести к увеличению периода колебаний маятника. С другой стороны, большая масса может также увеличить трение в точке подвеса маятника, что может замедлить его движение.

Масса также влияет на скорость, с которой маятник достигает своей максимальной высоты или амплитуды колебаний. Чем больше масса маятника, тем медленнее он будет подниматься и опускаться.

Однако следует отметить, что масса не является единственным фактором, влияющим на поведение нитяного маятника. Длина нити, угол отклонения, период колебаний и другие факторы также имеют значительное значение и должны быть учтены при изучении маятника.

Что собой представляет собой нитяной маятник

Главная цель Проверялкина – тренировка умения работать с параграфом: находить/выделять нужные по смыслу фрагменты, выбирать из нескольких подходящих фрагментов более удачный, многократно обращаться к тексту для поиска очередного ответа. В результате ваша зрительная память «схватывает» расположение в тексте важных моментов: определений, закономерностей, выводов; вы привыкаете к терминам и формулировкам. Другими словами, неоднократно перечитывая текст при поиске наилучшего ответа, вы полнее и обдуманнее воспринимаете физику.

Как и любой человек, Проверялкин «хочет» видеть не любой правильный ответ, а тот, который он считает наилучшим. Не расстраивайтесь, просто поищите другой ответ. Ведь разве плохо то, что вы будете знать несколько правильных ответов на один вопрос. Мы рекомендуем обсуждать задания с одноклассниками через наушники с микрофоном (или по телефону).

Важно: для Проверялкина правильным ответом является не только содержательно правильный, но и правильно «добытый». То есть ответы на задания Проверялкина нужно «перетаскивать» из параграфа, а не печатать «от себя» или копировать из других источников, например «готовых домашних заданий»

Давайте вспомним, какова главная цель вашей беседы с Проверялкиным? Правильно – тренировка умения работать с материалом параграфа учебника!

Для перехода к проверялкам по темам кликайте номера тем вверху: 01 02 03 04 05 и т.д.

Физика.ru • Клуб для учителей физики, учащихся 7-9 классов и их родителей

Математический нитяной маятник: основные принципы

Основные принципы, лежащие в основе математического нитяного маятника, включают:

1. Длина нити: математический нитяной маятник предполагает, что длина нити является постоянной и неизменной во время колебаний. Это позволяет упростить модель и получить аналитическое решение уравнений движения.

2. Конечная масса: математический нитяной маятник представляет точечную массу, которая сосредоточена в одной точке и не имеет размеров. Это объясняется тем, что модель идеализированная и не учитывает динамические эффекты, связанные с распределением массы.

3. Отсутствие сопротивления: модель предполагает, что нитяной маятник движется в отсутствие сопротивления воздуха или других трений. Это позволяет рассмотреть идеальные колебания и получить точные аналитические решения, которые легко применять в математических расчетах.

С помощью этих основных принципов математический нитяной маятник может быть полностью описан и исследован с математической точки зрения. Он является одной из основных моделей в физике и математике и относится к классу гармонических осцилляторов.

Расчет длины нити для маятника

Механизм работы нитяного маятника основан на принципах физики. Под действием силы тяжести, маятник осуществляет колебания, которые можно измерить с помощью времени.

Длина нити маятника играет важную роль в его движении. Для оптимального и стабильного колебания маятника необходимо правильно подобрать длину нити.

Длина нити маятника определяется таким образом, чтобы при колебании маятник описывал вертикальную траекторию. Это обеспечивает равномерное и предсказуемое движение маятника.

Для расчета длины нити маятника используется формула, которая связывает длину нити с периодом колебаний маятника и ускорением свободного падения под воздействием гравитации. Формула имеет вид:

l = (T^2 * g) / (4 * π^2)

Где l — длина нити маятника, T — период колебаний маятника, g — ускорение свободного падения, π — математическая константа, равная примерно 3,14.

Исходя из данной формулы, можно рассчитать оптимальную длину нити для маятника, чтобы достичь желаемого результата.

Расчет длины нити маятника является важным шагом при создании и использовании данного устройства. Правильное определение длины нити обеспечивает стабильное и безопасное движение маятника.

Влияние массы маятника

Амплитуда колебаний и время периода зависят от массы маятника. Чем больше масса маятника, тем меньше будет его амплитуда колебаний и больше время периода. Это связано с взаимодействием между гравитацией и массой маятника.

Масса маятника определяет скорость его движения и силу, с которой он действует на нить. Чем больше масса маятника, тем больше гравитационная сила, действующая на него. Поэтому маятник с большей массой будет двигаться медленнее и иметь меньшую амплитуду колебаний.

Таким образом, масса маятника влияет на его движение и колебания. При увеличении массы маятника, амплитуда колебаний уменьшается, а время периода увеличивается. И наоборот, при уменьшении массы маятника, амплитуда колебаний увеличивается, а время периода уменьшается.

Влияние ускорения свободного падения

Ускорение свободного падения определяет скорость с которой тела падают под воздействием силы тяжести. Величина этого ускорения примерно равна 9,8 м/с² на поверхности Земли. Маятник, будучи подвешенным на нити, подвержен воздействию этого ускорения, которое влияет на его движение и колебания.

Ускорение свободного падения влияет на период колебаний маятника. Период — это время, за которое маятник совершает одно полное колебание. При увеличении ускорения свободного падения, период колебаний становится короче. Это связано с тем, что при большем ускорении маятник быстрее преодолевает вертикальное расстояние и совершает больше колебаний за единицу времени.

Кроме того, ускорение свободного падения влияет на амплитуду маятника. Амплитуда представляет собой максимальное отклонение маятника от его вертикального положения равновесия. При увеличении ускорения свободного падения, амплитуда маятника увеличивается. Это происходит из-за того, что большая сила гравитации тянет маятник сильнее к своему вертикальному положению, что приводит к более сильному отклонению от него.

Итак, ускорение свободного падения играет важную роль в механизме работы нитяного маятника. Оно определяет скорость, период и амплитуду колебаний маятника. Понимая эту взаимосвязь, можно более полно осознать физические принципы, которые лежат в основе движения маятника.

2.3. Свободные колебания. Математический маятник window.top.document.title = «2.3. Свободные колебания. Математический маятник»;

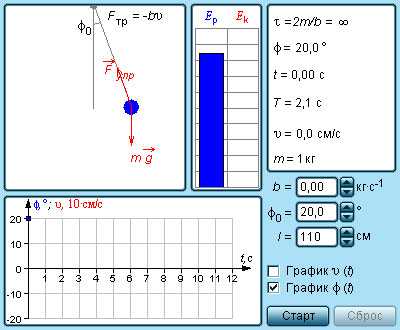
Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол φ появляется касательная составляющая силы тяжести F_τ = –mg sin φ (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.

Рисунок 2.3.1.Математический маятник. φ – угловое отклонение маятника от положения равновесия, x = lφ – смещение маятника по дуге

Если обозначить через x линейное смещение маятника от положения равновесия по дуге окружности радиуса l, то его угловое смещение будет равно φ = x / l. Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:

Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению x, а

Только в случае малых колебаний, когда приближенно можно заменить на математический маятник является гармоническим осциллятором, т. е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка 15–20°; при этом величина отличается от не более чем на 2 %. Колебания маятника при больших амплитудах не являются гармоническими.

Для малых колебаний математического маятника второй закон Ньютона записывается в виде

Таким образом, тангенциальное ускорение a_τ маятника пропорционально его смещению x, взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:

Эта формула выражает собственную частоту малых колебаний математического маятника.

Следовательно,

Модель. Математический маятник

Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим (рис. 2.3.2). Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс C физического маятника находится ниже оси вращения О на вертикали, проходящей через ось. При отклонении маятника на угол φ возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:

Здесь d – расстояние между осью вращения и центром масс C.

Рисунок 2.3.2.Физический маятник

Знак «минус» в этой формуле, как обычно, означает, что момент сил стремится повернуть маятник в направлении, противоположном его отклонению из положения равновесия. Как и в случае математического маятника, возвращающий момент M пропорционален sin φ. Это означает, что только при малых углах φ, когда sin φ ≈ φ, физический маятник способен совершать свободные гармонические колебания. В случае малых колебаний

см. §1.23

εIO

Здесь ω – собственная частота малых колебаний физического маятника.

Следовательно,

Более строгий вывод формул для ω и T можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение ε есть вторая производная углового смещения φ по времени:

Поэтому уравнение, выражающее второй закон Ньютона для физического маятника, можно записать в виде

Это уравнение свободных гармонических колебаний (). Коэффициент в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.

По теореме о параллельном переносе оси вращения (теорема Штейнера) момент инерции I можно выразить через момент инерции I_C относительно оси, проходящей через центр масс C маятника и параллельной оси вращения:

Окончательно для круговой частоты ω свободных колебаний физического маятника получается выражение:

Колебательное движение

В самом широком смысле, колебательное движение – это любое движение, повторяющееся с течением времени. Например, птица, машущая крыльями вверх-вниз, совершает ими колебательные движения. Ребенок, качающийся на качелях, тоже совершает колебательные движения. Игла швейной машины при шитье – тоже.

Но как же так, ведь в названных примерах тела движутся абсолютно по-разному? Крылья птицы и игла швейной машины движутся вертикально вверх-вниз (прямолинейно), ребенок на качелях движется горизонтально и по дуге (криволинейно)

Это все неважно. Главный признак колебательного движения – его повторяемость через определенный промежуток времени, то есть через период колебаний

Как сделать нитяной маятник своими руками?

Нитяной маятник – это простое устройство, которое представляет собой вертикально подвешенную нить, украшенную грузом внизу. Это устройство может использоваться для различных целей, включая демонстрацию физических законов и проведение научных экспериментов.

Чтобы сделать нитяной маятник своими руками, вам потребуется следующее:

• Нить или шнур достаточной длины
• Груз, например, крепкий предмет или маленькая бутылка с песком
• Крюк или крепление для подвешивания нити

Шаги по созданию нитяного маятника:

1. Присоедините нить к крюку или креплению так, чтобы она была прочно закреплена и свободно висела вниз.
2. Привяжите груз к нижнему концу нити. Убедитесь, что груз находится на достаточной высоте от пола.
3. Установите крюк или крепление так, чтобы нить была натянута и маятник свободно двигался.

После завершения этих шагов, вы получите нитяной маятник, который может использоваться для исследования физических явлений, таких как колебания и периодические движения. Вы можете изменять длину нити, чтобы изучать влияние длины на колебания маятника.

Преимущества и применение нитяного маятника: Преимущества Применение

Простота конструкции и использования Демонстрация физических законов в учебных целях

Доступность материалов Проведение научных экспериментов дома или в классе

Возможность изменять параметры маятника Исследование влияния длины, массы и других факторов на колебания маятника

Нитяной маятник – интересное и полезное устройство, которое позволяет изучать законы физики. Создайте свой собственный нитяной маятник и начните проводить интересные эксперименты уже сегодня!