Центральная симметрия — понятие, свойства и примеры фигур

Содержание

• Слайд 1

• Слайд 2

• Слайд 3

  • Понятие симметрии хорошо знакомо и играет важную роль в повседневной жизни. Многим творениям человеческих рук умышленно придается симметричная форма как из эстетических, так и практических соображений.
  • В древности слово «симметрия» употреблялось как «гармония», «красота». Действительно, по-гречески оно означает «соразмерность, пропорциональность, одинаковость в расположении частей».

• Слайд 4

  • Зеркальная симметрия
  • Двусторонняя симметрия
  • Осевая симметрия
  • Параллельный перенос
  • Центральная симметрия

• Слайд 5

  • Отражательная симметрия или осевая симметрия — вид движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии. Например, плоская фигура прямоугольник в пространстве осесимметрична и имеет 3 оси симметрии (две — в плоскости фигуры), если это не квадрат.
  • Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию (другие термины — радиальная, аксиальная, лучевая симметрии) относительно поворотов вокруг прямой. При этом тело (фигуру, задачу, организм) называют осесимметричными, если они переходят в себя при любом (например, малом) повороте вокруг этой прямой. В этом случае, прямоугольник не будет осесимметричным телом, но конус будет.
  • Применительно к плоскости эти оба вида симметрии совпадают (считаем, что ось тоже принадлежит этой плоскости).

• Слайд 6

• Слайд 7

• Слайд 8

• Слайд 9

• Слайд 10

  • Двусторонняя симметрия — симметрия зеркального отражения, при которой объект имеет одну плоскость симметрии, относительно которой две его половины зеркально симметричны. Если на плоскость симметрии опустить перпендикуляр из точки а и и затем из точки О на плоскости симметрии продолжить его на длину аО, то он попадёт в точку а1, во всем подобную точке а. Ось симметрии у билатерально симметричных объектов отсутствует. У животных билатеральная симметрия проявляется в схожести или почти полной идентичности левой и правой половин тела. При этом всегда существуют случайные отклонения от симметрии (например, различия в папиллярных линиях, ветвлении сосудов и расположении родинок на правой и левой руках человека). Часто существуют небольшие, но закономерные различия во внешнем строении (например, более развитая мускулатура правой руки у праворуких людей) и более существенные различия между правой и левой половиной тела в расположении внутренних органов. Например, сердце у млекопитающих обычно размещено несимметрично, со смещением влево.
  • У животных появление билатеральной симметрии в эволюции связано с ползанием по субстрату (по дну водоема), в связи с чем появляются спинная и брюшная, а также правая и левая половины тела. В целом среди животных билатеральная симметрия более выражена у активно подвижных форм, чем у сидячих. Билатеральная симметрия свойственна всем достаточно высокоорганизованным животным, кроме иглокожих. В других царствах живых организмов билатеральная симметрия свойственна меньшему числу форм. Среди протистов она характерна для дипломонад (например, лямблий), некоторых- форм трипаносом, бодонид, раковинок многих фораминифер. У растений билатеральную симметрию имеет обычно не весь организм, а его отдельные части — листья или цветки. Билатерально симметричные цветки ботаники называют зигоморфными.

• Слайд 11

• Слайд 12

  Зеркальная симметрия, это вид симметрии, часто наблюдаемый в природе и в созданных человеком вещах, — так называемая зеркальная симметрия. Человеческое тело обладает (приближенно) зеркальной симметрией относительно вертикальной оси. В зеркале правая и левая руки и другие части тела меняются местами, но видимое нами зеркальное отражение узнаваемо. Многие архитектурные сооружения, например арки или соборы, обладают зеркальной симметрией.

• Слайд 13

• Слайд 14

• Слайд 15

• Слайд 16

• Слайд 17

• Слайд 18

  Центральная симметрия

  Симметрия относительно точки или центральная симметрия — это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону центра симметрии, соответствует другая точка, расположенная по другую сторону центра. При этом точки находятся на отрезке прямой, проходящей через центр, делящий отрезок пополам.

• Слайд 19

• Слайд 20

• Слайд 21

• Слайд 22

• Слайд 23

• Слайд 24

Посмотреть все слайды

Введение

Темой данной работы является понятие симметрии. Есть мнение, что симметрия играет ведущую, хотя и не всегда осознанную роль в современной науке, искусстве, технике и окружающей нас жизни.

Что же такое симметрия? Почему симметрия буквально пронизывает весь окружающий нас мир?

Существует, в принципе, две группы симметрий. К первой группе относится симметрия положений, форм, структур. Это та симметрия, которую можно непосредственно видеть. Она может быть названа геометрической симметрией.

Вторая группа характеризует симметрию физических явлений и законов природы. Эта симметрия лежит в самой основе естественнонаучной картины мира: ее можно назвать физической симметрией.

Цель : Изучить проявления симметрии в различных областях жизни человека и общества.

1. Определить основные признаки понятия симметрии.

2. Определить присутствие симметрии в живой и не живой природе, в лингвистике, в искусстве.

3. Изучить достоинства симметричных предметов в образном восприятии человека.

Актуальность обусловлена тем, что симметрия окружает человека, находя свое проявление как в живой, так и не в живой природе, а также большинстве творений человека: в архитектуре, в искусстве и т.д

Объяснение законов симметрии важно для понимая красоты и гармонии. Результаты проекта будут интересны для учащихся средней школы

В данной работе я исследую геометрическую симметрию и покажу, что геометрическая симметрия присутствует во всем, что нас окружает, с чем мы сталкиваемся постоянно в обыденной жизни.

Понятие правильного многогранника, теорема о правильных многогранниках

Определение.

Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники, а в каждой вершине сходится одинаковое число ребер.

Теорема.

Не существует правильного многогранника, гранями которого являются правильные n-угольники при .

Доказательство:

Рассмотрим случай, когда  – правильный шестиугольник. Все его внутренние углы равны :

Тогда при  внутренние углы будут  и больше.

В каждой вершине многогранника сходятся не менее трех ребер, значит, в каждой вершине содержится не менее трех плоских углов. Их общая сумма (при условии, что каждый больше либо равен ) больше либо равна . Это противоречит утверждению: в выпуклом многограннике сумма плоских всех углов при каждой вершине меньше .

Теорема доказана.

Интересные факты о центральной симметрии

Вся окружающая нас природа – сплошная центральная симметрия. Многие растения и насекомые обладают центральной симметрией. 

Практически у каждого фрукта есть своя симметрия. Например, кокос в разрезе представляет собой окружность с центром в некоторой точке. 

Ещё один очевидный пример – бабочка. 

Великолепные узоры на её крылышках – четкая и яркая симметрия. 

Каждый знает, что видовое разнообразие морских ракушек бесконечно. Наверняка, вы сможете найти несколько как с осевой, так и центральной симметрией.

Великолепные примеры с элементами центральной симметрии можно наблюдать и в архитектуре. Потолки различных храмов и церквей украшаются орнаментами, основой которых является центральная симметрия. 

Собор Парижской Богоматери имеет прекрасный, утончённый узор, основанный на центральной симметрии.

Рукодельницы в своих произведениях искусства применяют симметрию, которая заметна в удивительных и затейливых узорах.

Таким образом, центральная симметрия – основа, которая составляет природу, архитектуру и даже иногда музыку. Именно это проявление так радует человеческий глаз при появлении первых снежинок или при знакомстве с сооружениями архитектуры.

Сообщение по теме

Осевая и центральная симметрия — это два важных понятия в геометрии, которые описывают отношения между фигурами.

Осевая симметрия — это свойство фигуры сохраняться при отражении относительно оси симметрии. Ось симметрии — это линия, которая делит фигуру на две равные части (зеркальные отображения друг друга). Примеры фигур с осевой симметрией включают прямоугольник, квадрат, круг и другие. В некоторых случаях ось симметрии может быть вымышленной или не являться прямой линией.

Центральная симметрия — это свойство фигуры сохраняться при повороте на 180 градусов относительно центра симметрии. Центр симметрии — это точка, которая является центром поворота. Примеры фигур с центральной симметрией включают круг, звезду и др.

Осевая и центральная симметрия являются важными концепциями в математике и имеют широкое применение в различных областях, включая архитектуру, дизайн и физику. Например, осевая симметрия используется при проектировании зеркал, а центральная симметрия — при изучении свойств магнитов.

Таким образом, понимание осевой и центральной симметрии имеет большое значение для понимания принципов геометрии и их применения в реальном мире.

Что такое центральная симметрия

Точки А и А1 называются симметричными относительно точки О, если О — середина АА1.

Рисунок 1. Центральная симметрия в снежинке. 

Например, центр симметрии:

• окружности — центр окружности;
• параллелограмма — точка пересечения его диагоналей;
• прямой — любая точка прямой, то есть бесконечное множество центров симметрии.

Фигуру можно называть симметричной относительно центра симметрии, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре. 

Фигуры, симметричные относительно некоторой точки, равны. 

Одним из первых ученых, подробно изучавшим центральную симметрию, был выдающийся немецкий математик Феликс Клейн. При изучении геометрии, утверждал Клейн, нужно рассматривать не только объекты (треугольники, окружности и т.д.), но и перемещения.

В классической геометрии Евклида более двух тысяч лет под перемещениями понимались только движения твердого тела: можно взять фигуру и поместить ее копию в новое место. При подходе Клейна геометрия охватывает гораздо более широкий класс задач, чем в классическом понимании. 

1. Доказательство с помощью векторов: Пусть точки A и B отобразились соответственно на A1 и B1, а О — центр симметрии. Тогда, из определения центральной симметрии, векторы OA1 = -OA, OB1 = -OB.

Рассмотрим вектор A1B1 = OB1 — OA1= -(OB)-(-OA)= -OB+OA= -(OB-OA)= -AB.

Следовательно, центральная симметрия является движением, изменяющим направление на противоположное.

2. Доказательство геометрическим методом. 

Дано: точки А и В, точка О — центр, А1, В1 — образы исходных точек, АО=ОА1, ВО=ОВ1. 

Доказать, что АВ=А1В1. 

Рисунок 2. 

Решение: 

Рассмотрим ΔAOB и ΔA1OB1 (рисунок 2). По условию: 

1. AO=A1O.
2. BO=B1O.
3. 3. ∠AOB=∠A1OB1, так как это вертикальные углы.

1,2,3 ⇒ ΔAOB = ΔA1OB ⇒ AB=A1B1. Что и требовалось доказать. 

Свойства центральной симметрии

Основные свойства следующие:

1. Центральную симметрию называют движением, при котором соответствующие точки также остаются симметричными, то есть расстояние между ними остаётся прежним.

Посмотрим на рисунок. Треугольники АВС и А₁В₁С₁
симметричны в пространстве относительно точки О. При каком либо преобразовании пространства сохраняются условия: АО=А₁О, ВО=В₁О, СО=С₁О. Значит, картинка остаётся той же.

Однако если представить геометрическую фигуру в виде векторов, то при преобразовании пространства эти векторы поменяют свои направления;

2. Центральная симметрия имеет только одну центральную точку, которая является неподвижной при преобразовании пространства;

3. Если прямая проходит через центр симметрии, то она соответствует самой себе, то есть симметрична;

4. Центральная симметрия переводит прямую, не проходящую через центр симметрии, в параллельную ей прямую.

Доказывается это свойство достаточно просто. Для этого нужно построить две параллельные прямые АВ и А₁В₁ относительно точки О_.

Далее соединяем симметричные точки и получаем отрезки АА₁ и ВВ₁. Далее легко заметить, что отрезки АО и А₁О будут равны. Соответственно равны и отрезки ВО и В₁О. Углы, которые образуются при пересечении двумя прямыми точки О также равны. 

Значит, треугольники равны по двум сторонам и углу между ними. Следовательно, равны углы А,А₁ и В,В_1. Значит они являются накрест лежащими при секущих АА₁ и ВВ₁. Задача решена, АВ и А₁В₁ параллельны;

5. При центральной симметрии отрезки симметричны отрезкам, лучи симметричны лучам, прямые симметричны прямым.

Презентация на тему: » Симметрия в нашей жизни Геометрия Симметрия в нашей жизни Геометрия.» — Транскрипт:

1

Симметрия в нашей жизни Геометрия Симметрия в нашей жизни Геометрия

2

научить распознавать симметричные фигуры среди других; познакомить учащихся с использованием симметрии в природе, быту, искусстве, технике; развивать умения анализировать и сравнивать предметы; ЗАДАЧИ:

3

Симметричность точек относительно прямойСимметричность точек относительно прямой Симметричность фигуры относительно прямойСимметричность фигуры относительно прямой Симметричность точек относительно точкиСимметричность точек относительно точки Симметричность фигуры относительно точкиСимметричность фигуры относительно точки Симметрия вокруг насСимметрия вокруг нас Математики о симметрииМатематики о симметрии

4

Симметрия (от греческого symmetria — «соразмерность») — понятие, означающее сохраняемость, повторяемость, «инвариантность» каких-либо особенностей структуры изучаемого объекта при проведении с ним определенных преобразований». СИММЕТРИЯ

5

Трансляционная симметрия Центральная симметрия Осевая симметрия Зеркальная симметрия Поворот Параллельный перенос Скользящая симметрия

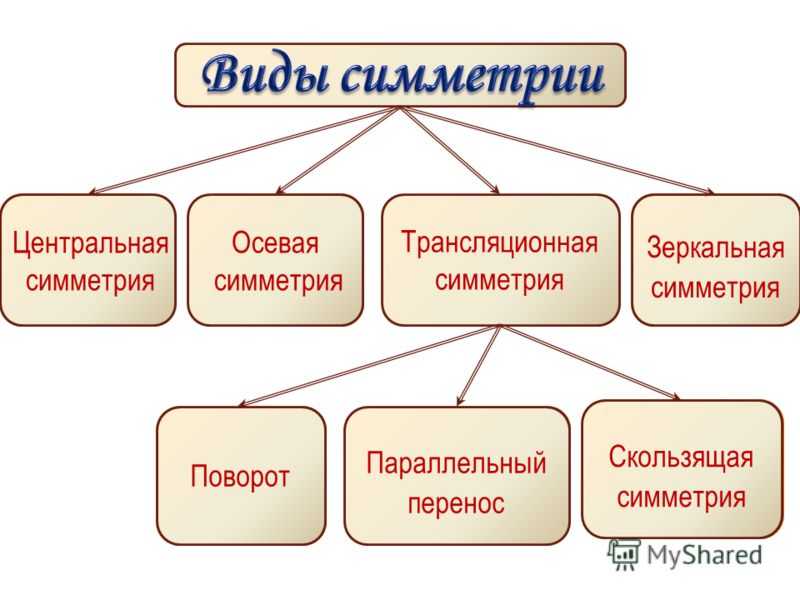
6

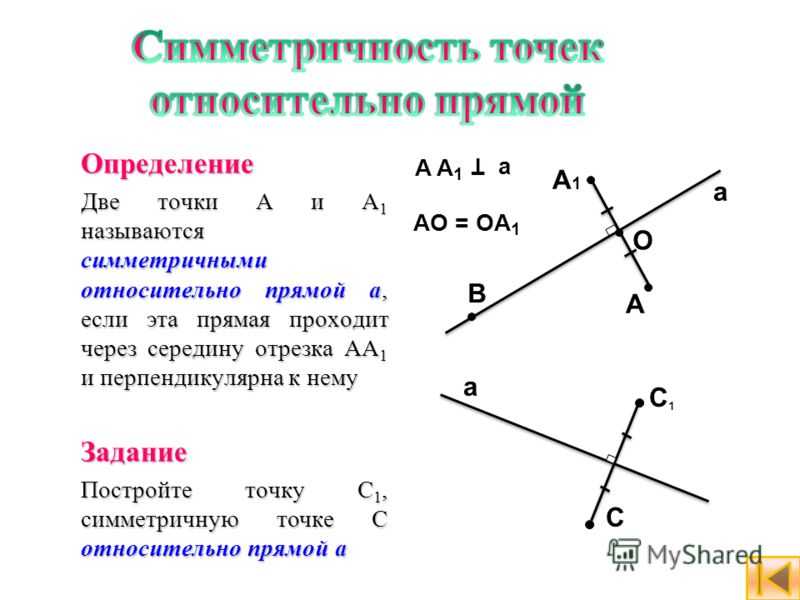
Определение Две точки А и А 1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему Задание Постройте точку C 1, симметричную точке C относительно прямой а A1A1 A a O B A A1A A1 a Т AO = OA 1 C1C1 a C

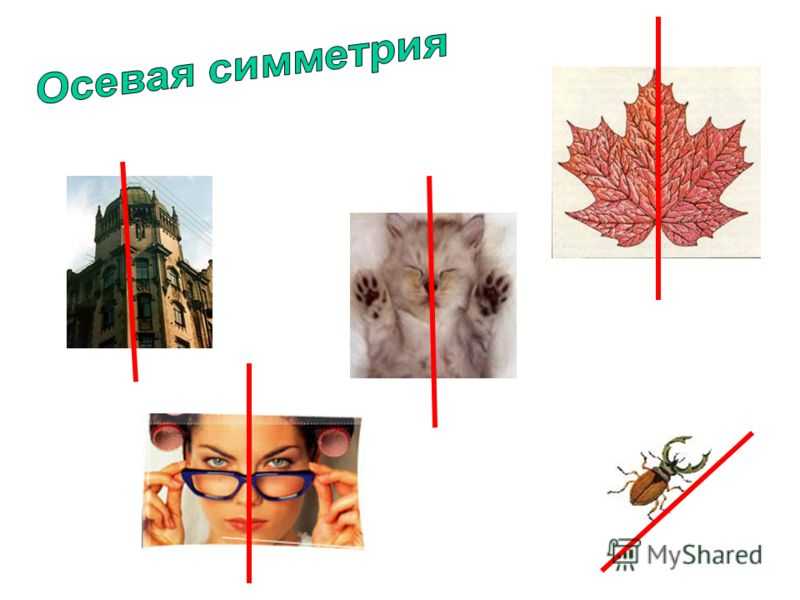
7

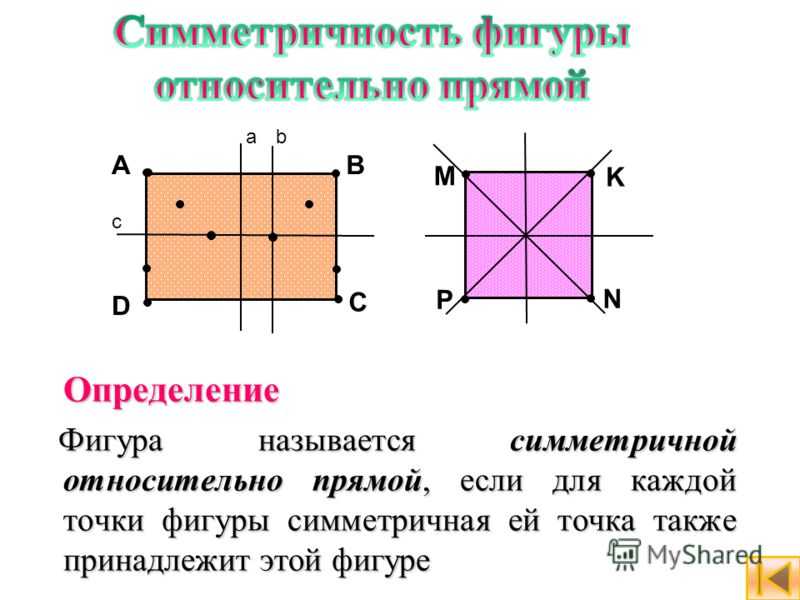
Определение Фигура называется симметричной относительно прямой, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре Фигура называется симметричной относительно прямой, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре А D B C M K N P ab c

8

Какие из данных фигур имеют ось симметрии? Сколько?

9

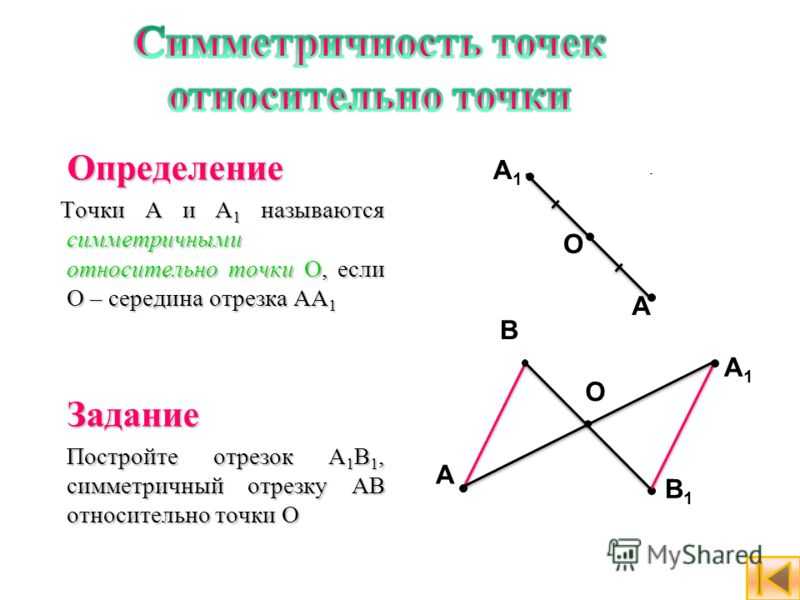
Определение Точки A и A 1 называются симметричными относительно точки О, если О – середина отрезка AA 1 Точки A и A 1 называются симметричными относительно точки О, если О – середина отрезка AA 1Задание Постройте отрезок A 1 B 1, симметричный отрезку AB относительно точки О Постройте отрезок A 1 B 1, симметричный отрезку AB относительно точки О A O A B B1B1 O A1A1 A1A1

10

Определение Фигура называется симметричной относительно точки, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре. Фигура называется симметричной относительно точки, если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре. Какие из данных фигур имеют центр симметрии? A B C D O

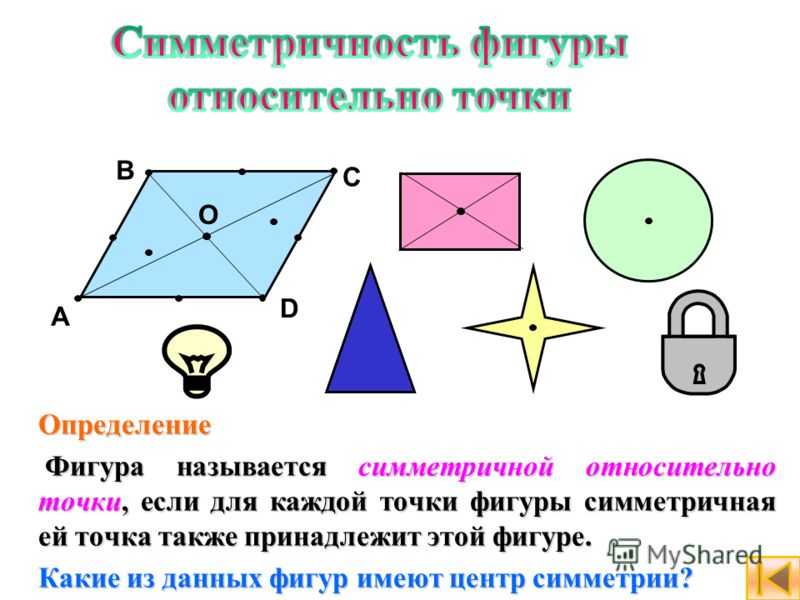
13

Нетрадиционные виды симметрии Винтовая симметрия Симметрия поворота Переносная симметрия

14

Винтовая симметрия

15

Переносная симметрия или скользящее преобразование

16

Симметрия поворота

19

Часто такую симметрию называют зеркальной. А зеркало не просто копирует объект, но и меняет местами передние и задние части объекта по отношению к зеркалу. Дубаи Башни Эмиратов Соловецкий монастырь Германия Гамбург

21

Симметрия танца

22

Симметрия в литературе Палиндром — это абсолютное проявление симметрии в литературе. Например: «А луна канула», «А роза упала на лапу Азора». Палиндром В.Набокова: Я ел мясо лося, млея… Рвал Эол алоэ, лавр. Те ему: «Ишь! И умеет Рвать!» Он им: «Я — минотавр!» Он им: «Я — минотавр!» назад

24

Математик любит прежде всего симметрию Максвелл Д. Максвелл Д. Красота тесно связана с симметрией Вейль Г. Вейль Г. Симметрия … является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство Вейль Г. Вейль Г. Для человеческого разума симметрия обладает, по — видимому, совершенно особой притягательной силой Фейнман Р. Фейнман Р.

25

Заключение Симметрия играет огромную роль в искусстве: в архитектуре, в музыке, в поэзии; природе: у растений и животных; в технике, в быту. Симметрия играет огромную роль в искусстве: в архитектуре, в музыке, в поэзии; природе: у растений и животных; в технике, в быту.

26

Ответьте на вопросы: С каким понятием мы сегодня познакомились? Какие виды симметрии вы запомнили? Что нового вы узнали?

Виды симметрии, определения, примеры

Как и в планиметрии, в пространстве мы будем рассматривать симметрию относительно точки и относительно прямой, но дополнительно появится симметрия относительно плоскости.

Определение.

Точки А и  называются симметричными относительно точки О (центра симметрии), если О – середина отрезка . Точка О симметрична сама себе.

Чтобы для заданной точки А получить симметричную ей точку  относительно точки О, нужно провести прямую через точки А и О, отложить от точки О отрезок, равный ОА, и получить искомую точку  (рисунок 1).

Рис. 1. Симметрия относительно точки

Аналогично точки В и  симметричны относительно точки О, т. к. О – середина отрезка .

Так, задан закон, согласно которому каждая точка плоскости переходит в другую точку плоскости, и мы говорили, что при этом сохраняются любые расстояния, то есть .

Рассмотрим симметрию относительно прямой в пространстве.

Чтобы получить для заданной точки А симметричную точку относительно некоторой прямой а, нужно из точки А на прямую опустить перпендикуляр и отложить на нем равный отрезок (рисунок 2).

Рис. 2. Симметрия относительно прямой в пространстве

Определение.

Точки А и  называются симметричными относительно прямой а (ось симметрии) если прямая а проходит через середину отрезка  и перпендикулярна ему. Каждая точка прямой  симметрична сама себе.

Определение.

Точки А и  называются симметричными относительно плоскости  (плоскость симметрии) если плоскость  проходит через середину отрезка  и перпендикулярна ему. Каждая точка плоскости  симметрична сама себе (рисунок 3).

Рис. 3. Симметрия относительно плоскости

Некоторые геометрические фигуры могут иметь центр симметрии, ось симметрии, плоскость симметрии.

Вариант 2

Наверное, каждый слышал такие понятия, как «симметрия», «симметрично» и тому подобное. Но есть такие люди, которые не понимают значение данных синонимов. Так что же такое симметрия? Где ее применяют? И какие разновидности существуют?

Краткий экскурс о симметрии в общих чертах.

Постараюсь объяснить понятие симметрии на некотором примере. Представьте обыкновенную бабочку. Так, а теперь надо провести через нее линию. Когда линия окончательно проведена, необходимо посмотреть на правую и левую части рисунка. Если эти 2 части рисунка одинаковы по размерам и пропорциям, то это можно называть симметричной моделью. Короче говоря, симметрия – это полная соразмерность частей тела по отношению к линии. Где же применяется симметрия? Ну, симметрия встречается везде, где только можно. Геометрия, физика, биология, химия, культура – все это содержит симметрию, причем каждая отличается друг от друга. Еще существует понятие асимметрии. То есть, отсутствие правильной соразмерности. Еще стоит отметить, что симметрия не всегда бывает точной.

Некоторые виды симметрии, их характеристика и применение.

Всего наберется с десяток разных видов симметрий. Но рассмотреть необходимо только те, которые часто встречаются. Сразу стоит сказать, что обе из них находят применение в решении задач по геометрии. Итак, вот 2 главных вида симметрии:

Осевая симметрия.

Этот вид симметрии делится на 4 группы, отличающиеся друг от друга.

1) Отражательная симметрия – это зеркальное движение, в котором точки, не перемещающиеся никуда, соединены в одну линию – ось симметрии. Прямоугольник и параллелограмм – отличные примеры.

2) Вращательная симметрия – это осевая симметрия, которая относительна поворотам вокруг оси.

3) Осевая симметрия n – го порядка – это симметрия относительно поворотов на 360 градусов вокруг оси.

4) Зеркально поворотная осевая симметрия n – го порядка – то же самое, только перпендикулярно оси.

Центральная симметрия.

Это преобразование, при котором каждая точка А переходит в точку А1, при этом она симметрична предыдущей относительно оси О. Данная симметрия – это, по сути, тот же поворот на 180 градусов в планиметрии. Центральную симметрию от осевой отличает то, что в первом случае присутствует движение.

Геометрия 10 класс

«Равносторонние многоугольники» — Тетраэдр имеет 4 грани, 4 вершины и 6 ребер. Додекаэдр имеет 12 граней, 20 вершин и 30 ребер. Гексаэдр (Куб) Куб составлен из шести квадратов. Октаэдр имеет 8 граней, 6 вершин и 12 ребер. Икосаэдр имеет 20 граней, 12 вершин и 30 ребер. Октаэдр Октаэдр составлен из восьми равносторонних треугольников. Правильные Многоугольники. Тетраэдр гексаэдр октаэдр икосаэдр додекаэдр. Таким образом, куб имеет 6 граней, 8 вершин и 12 ребер.

«Декартова система» — Координаты вектора. Декартова система координат. Понятие системы координат. Рене Декарт. Координаты любой точки. Координаты точки. Прямоугольная система координат. Вопросы для заполнения. Введение декартовых координат в пространстве. Определение декартовой системы.

«Методы построения сечений многогранников» — Решения варианта. Параллелепипед. Блиц-опрос. Закрепление полученных знаний. Построить сечение многогранника. Правила для самоконтроля. Пересекаются ли прямые. Самостоятельная работа. Задачи. Свойство. Законы геометрии. Прямые. Задача. Любая плоскость. Корабль. Ошибка. Простейшие задачи. Сечения параллелепипеда. Разрезы образовали пятиугольник. Точки пересечения. Взаимное расположение плоскости и многогранника.

«Параллельность плоскостей» — Невозможные структуры. Плоскости. Пересекающиеся прямые. Сова. Теоремы. Середины. Признак параллельности. Плоскости параллельны. Параллельные плоскости в технике. Плоскости называются параллельными, если они не пересекаются. Параллельные плоскости в быту. Параллельный мир. Доказательство от противного. Могут ли прямая и плоскость не иметь общих точек. Параллельность плоскостей. Отрезки. Параллельные плоскости в искусстве.

«Тела Платона» — Правильные многогранники. Правильные многогранники или тела Платона. Тетраэдр. Гексаэдр. Додекаэдр. Дуальность. Октаэдр. Платон. Тела Платона. Икосаэдр.

«Основные аксиомы стереометрии» — Аксиома. Первые уроки стереометрии. Четыре равносторонних треугольника. Следствия из аксиом. Геометрические тела. Плоскость. Аксиомы стереометрии. Источники и ссылки. Следствия из аксиом стереометрии. Изображения пространственных фигур. Пирамида Хеопса. Геометрия. Древняя китайская пословица. Плоскости имеют общую точку. Предмет стереометрии. Основные фигуры в пространстве. Точки прямой лежат в плоскости.

«Геометрия 10 класс»

Элементы симметрии фигур

Определение.

Точка О называется центром симметрии фигуры если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.

Например, в параллелограмме и параллелепипеде точка пересечения всех диагоналей является центром симметрии. Проиллюстрируем для параллелепипеда.

Рис. 4. Центр симметрии параллелепипеда

Так, при симметрии относительно точки О в параллелепипеде  точка А переходит в точку , точка В – в точку  и т. д., таким образом, параллелепипед переходит сам в себя.

Определение.

Прямая  называется осью симметрии фигуры если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.

Например, каждая диагональ ромба является для него осью симметрии, ромб переходит сам в себя при симметрии относительно любой из диагоналей.

Рассмотрим пример в пространстве – прямоугольный параллелепипед (боковые ребра перпендикулярны основаниям, в основаниях – равные прямоугольники). Такой параллелепипед имеет оси симметрии. Одна из них проходит через центр симметрии параллелепипеда (точку пересечения диагоналей) и центры верхнего и нижнего оснований.

Определение.

Плоскость  называется плоскостью симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры.

Например, прямоугольный параллелепипед имеет плоскости симметрии. Одна из них проходит через середины противоположных ребер верхнего и нижнего оснований (рисунок 5).

Рис. 5. Плоскость симметрии прямоугольного параллелепипеда

Элементы симметрии присущи правильным многогранникам.

Слайды и текст этой презентации

Слайд 3Цель урока: Ознакомление с понятием симметрии в пространстве и с

пять видов правильных многогранников

магические свойства. Древнегреческий ученый и философ Платон (IV–V в до

н. э.) считал, что эти тела олицетворяют сущность природы. В своем диалоге «Тимей» Платон говорит, что атом огня имеет вид тетраэдра, земли – гексаэдра (куба), воздуха – октаэдра, воды – икосаэдра. В этом соответствии не нашлось места только додекаэдру и Платон предположил существование еще одной, пятой сущности – эфира, атомы которого как раз и имеют форму додекаэдра. Ученики Платона продолжили его дело в изучении перечисленных тел. Поэтому эти многогранники называют платоновыми телами.

Слайд 8Доказать, что не существует правильного многогранника, у которого гранями являются

правильные n-угольники при n≥6.
Угол правильного многоугольника вычисляется по формуле αn

= 1800(n – 2)/n. При каждой вершине многогранника не меньше 3 плоских углов, и их сумма должна быть меньше 360о. При n=3, когда гранями многогранника служат правильные треугольники, имеем: α3=60о, 60о•3=180о

– куб.

Слайд 10Если n=5, то есть грани многогранника – правильные пятиугольники, то

α5=108о, 108о•3=324о360o, и поэтому в этом случае также имеем

только один правильный многогранник – додекаэдр. Если n≥6, то αn≥120o, αn•3≥360o, и, следовательно, не существует правильного многогранника, гранями которого служат правильные n-угольники при n≥6.

Слайд 11Правильный тетраэдр не имеет центра симметрии. Прямая, проходящая через середины

двух противоположных ребер, является его осью симметрии.
Плоскость а,

проходящая через ребро АВ перпендикулярно к противоположному ребру СВ правильного тетраэдра АВСВ, является плоскостью симметрии. Правильный тетраэдр имеет три оси симметрии и шесть плоскостей симметрии.

Слайд 12 Куб имеет один центр симметрии — точку пересечения его

диагоналей. Прямые а и Ь, проходящие соответственно через центры противоположных

граней и середины двух противоположных ребер, не принадлежащих одной грани, являются его осями симметрии. Куб имеет девять осей симметрии. Все оси симметрии проходят через центр симметрии. Плоскостью симметрии куба является плоскость, проходящая через любые две оси симметрии. Куб имеет девять плоскостей симметрии

симметрии и несколько осей и плоскостей симметрии.
Попробуйте

подсчитать их число.

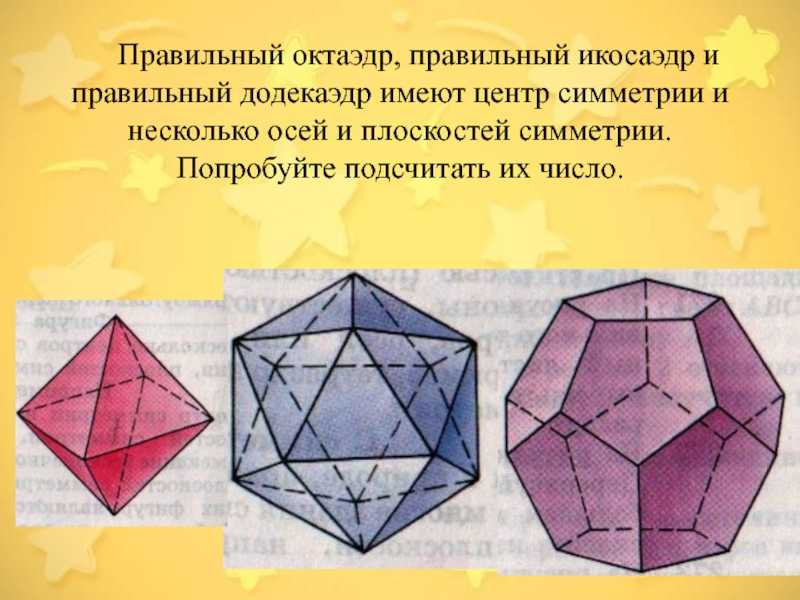
многогранников, изготовить модели; №283, 284.
 

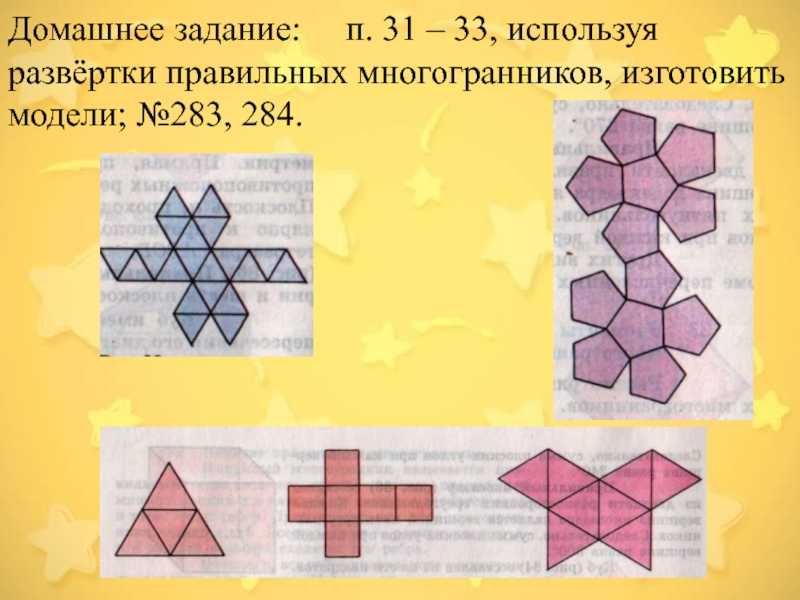
Слайд 16Список использованной литературы:

1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселёва

Л.С., Позняк Э.Г. Геометрия 10-11, М.,
«Просвещение» 2004г.
2. Бутузов В.Ф., Саакян

Примеры правильных многогранников

Куб (рисунок 6):

Рис. 6. Куб

-куб составлен из шести квадратов; квадрат – это правильный многоугольник;

-каждая вершина – это вершина трех квадратов, например вершина А – общая для граней-квадратов ABCD, ;

-сумма всех плоских углов при каждой вершине составляет , т. к. состоит из трех прямых углов. Это меньше , что удовлетворяет понятию правильного многогранника;

-куб имеет центр симметрии – точка пересечения диагоналей;

-куб имеет оси симметрии, например прямые а и b (рисунок 6), где прямая а проходит через середины противоположных граней, а b – через середины противоположных ребер;

-куб имеет плоскости симметрии, например плоскость, которая проходит через прямые а и b.

2. Правильный тетраэдр (правильная треугольная пирамида, все ребра которой равны между собой):

Рис. 7. Правильный тетраэдр

-правильный тетраэдр составлен из четырех равносторонних треугольников;

-в каждой вершине сходятся по три ребра;

-сумма всех плоских углов при каждой вершине составляет , т. к. правильный тетраэдр состоит из трех плоских углов по . Это меньше , что удовлетворяет понятию правильного многогранника;

— правильный тетраэдр имеет оси симметрии, они проходят через середины противоположных ребер, например прямая MN. Кроме того, MN – расстояние между скрещивающимися прямыми АВ и CD, MN перпендикулярно ребрам АВ и CD;

-правильный тетраэдр имеет плоскости симметрии, каждая проходит через ребро и середину противоположного ребра (рисунок 7);

-правильный тетраэдр не имеет центра симметрии.

3. Правильный октаэдр:

-состоит из восьми равносторонних треугольников;

-в каждой вершине сходятся по четыре ребра;

-сумма всех плоских углов при каждой вершине составляет , т. к. правильный октаэдр состоит из четырех плоских углов по . Это меньше , что удовлетворяет понятию правильного многогранника.

4. Правильный икосаэдр:

-состоит из двадцати равносторонних треугольников;

-в каждой вершине сходятся по пять ребер;

-сумма всех плоских углов при каждой вершине составляет , т. к. правильный икосаэдр состоит из пяти плоских углов по . Это меньше , что удовлетворяет понятию правильного многогранника.

5. Правильный додекаэдр:

-состоит из двенадцати правильных пятиугольников;

-в каждой вершине сходятся по три ребра;

-сумма всех плоских углов при каждой вершине составляет . Это меньше , что удовлетворяет понятию правильного многогранника.

Итак, мы рассмотрели виды симметрии в пространстве и дали строгие определения. Также определили понятие правильного многогранника, рассмотрели примеры таких многогранников и их свойства.

ИСТОЧНИК

http://interneturok.ru/ru/school/geometry/10-klass/mnogogranniki/simmetriya-v-prostranstve-ponyatie-pravilnogo-mnogogrannika

https://www.youtube.com/watch?v=vP2_C0N5cII

https://www.youtube.com/watch?v=fbJEG_klEvg

https://www.youtube.com/watch?v=KQVvIPgse98

http://ppt4web.ru/geometrija/pravilnye-mnogogranniki3.html

http://referatdoki.ru/konspekt/samostoyatelnaya-rabota/zashhita-proektov-pravilnye-mnogogranniki/

http://lusana.ru/presentation/5072

http://900igr.net/prezentatsii/geometrija/Simmetrija-pravilnykh-mnogogrannikov/Simmetrija-pravilnykh-mnogogrannikov.html

Заключение

Изучив и исследовав тему «Симметрии» я узнал, что помимо осевого, зеркального и центрального типов симметрии, которые мы изучаем в школьном курсе, существуют и другие виды симметрии, например, в природе — вращательная, винтовая, в кристаллография в целом — 32 вида.

Таким образом, изучая симметрию законов природы, рано или поздно можно глубже проникнуть в суть живого, объяснить ход эволюции и дать возможность человеку чаще применять эти законы симметрии в жизни.

Рассматривая архитектуру зданий, предметы декора и быта, технические изобретения, мы видим в них наличие центрального, поворотного, переносного, осевого и зеркального типов симметрии, дающих ощущение спокойной уверенности и эстетической привлекательности.

Симметрия, проявляясь в самых разнообразных объектах природного мира, несомненно, отражает его самые общие свойства. Поэтому изучение симметрии различных природных объектов и сравнение его (исследования) результатов — удобный и надежный инструмент для понимания гармонии мира.