Унарная система счисления: простое и эффективное представление чисел

Принцип работы унарной системы счисления

Принцип работы унарной системы счисления заключается в том, что числа представляются через повторение символа единицы. Таким образом, каждая цифра унарной системы счисления обозначает определенное количество единиц.

Например, число 3 в унарной системе счисления записывается как «111», где каждая единица представляет собой одно число. А число 7 записывается как «1111111».

Операции сложения и умножения в унарной системе счисления также основаны на принципе повторения символа единицы. Например, чтобы сложить два числа 3 и 4, нужно просто объединить их символы единицы и получить число 7.

Однако из-за своей простоты и ограниченности, унарная система счисления не является эффективным способом для работы с большими числами. Именно поэтому она редко применяется в настоящее время и используется в основном в учебных целях.

Последние заданные вопросы в категории Информатика

Информатика 22.10.2023 06:31 6 Тажетдинов Динислам

прошу помогите срочно, «Дані, які користувач свідомо вносить до мережних сервісів: створені ним сайт

Ответов: 1

Информатика 22.10.2023 06:29 26 Чернецова Анастасия

Помогите. пжрнтшршромлмлтл щт лм​

Ответов: 1

Информатика 22.10.2023 06:27 8 Косотуров Кирилл

Выберите логическое выражение, соответствующее более тёмной области диаграммы Эйлера — Венна.

Ответов: 1

Информатика 22.10.2023 06:24 22 Савина Яна

Толық аты-жөнің қанша бит, қанша байт болатынын есепте? срочно​

Ответов: 1

Информатика 22.10.2023 06:23 4 Вешняков Тимур

Пайтон черепашка Задание 1. Нарисовать олимпийские кольца с помощью библиотека turtle. Использоват

Ответов: 1

Информатика 22.10.2023 06:00 15 Романова Катя

Бит дегенiмiз не? ㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤㅤ​

Ответов: 2

Информатика 22.10.2023 05:55 26 Алавердян Илья

Стандарти якого коду вказано UTF32, UTF16, UTF8допоможіть будьласочка ​

Ответов: 2

Информатика 22.10.2023 05:54 24 Новарчук Никита

Python 2. Реалізувати функцію progressbar(), яка буде виконуватися при запуску бота from tqdm impo

Ответов: 1

Информатика 22.10.2023 05:31 29 Гайсанов Ахмед

Дам 50 баллов Обчисліть довжину двійкового коду в МБ деякого тексту, який складається з 3 сторінок,

Ответов: 1

Информатика 22.10.2023 05:29 17 Старий Денис

Напишіть програму, яка виконує поелементну суму двох списків та результат заносить до третього спи

Ответов: 1

Унарная система счисления: основные понятия

В унарной системе счисления нет понятий разрядов и порядков, как в десятичной системе счисления. Каждая единица в унарной системе имеет одинаковую ценность. Таким образом, число 3, например, будет представлено тройкой единиц: 111.

Унарная система счисления является самой простой системой счисления, но она имеет некоторые ограничения. Из-за отсутствия разрядов и порядков, представление больших чисел в унарной системе может быть очень неудобным и занимать много места.

Унарная система счисления использовалась в древности и в религиозных текстах для представления простых понятий или описания числа в соответствии с их символическим значением.

В современности унарная система счисления имеет ограниченное применение в некоторых областях информатики и математики, например, для демонстрации принципов работы компьютерных алгоритмов или для решения определенных задач.

Примеры использования унарной системы счисления

Унарная система счисления, хоть и не является практичной для повседневного использования, все же может быть полезной в некоторых специфических случаях. Вот несколько примеров использования унарной системы счисления:

Представление количества

Унарная система счисления может быть использована для представления количества объектов или событий. Например, если у вас есть 5 яблок, вы можете представить это в унарной системе счисления, используя 5 символов “1”. Таким образом, вы можете легко считать количество яблок, просто считая количество символов “1”.

Теоретические исследования

Унарная система счисления также может быть использована в теоретических исследованиях и математических доказательствах. Из-за своей простоты, она может быть полезна для иллюстрации некоторых концепций и свойств чисел. Например, унарная система счисления может быть использована для доказательства некоторых теорем или для иллюстрации алгоритмов и операций над числами.

Кодирование информации

В некоторых случаях, унарная система счисления может быть использована для кодирования информации. Например, в некоторых компьютерных алгоритмах или протоколах связи, унарное кодирование может быть использовано для представления определенных значений или состояний. Хотя это не является распространенным способом кодирования, в некоторых специализированных областях оно может быть полезным.

В целом, унарная система счисления имеет ограниченное применение и используется главным образом для простых задач или теоретических исследований. В повседневной жизни мы обычно используем более эффективные системы счисления, такие как десятичная или двоичная, для работы с числами и информацией.

Непозиционная система счисления

Для такой системы счисления количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.

Примерно в III тысячелетии до н.э. древние египтяне разработали десятичную непозиционную систему счисления, в которой для обозначения узловых чисел 1, 10, 100 использовались символы – иероглифы.

В большинстве непозиционных систем счисления новые числа образуются путём сложения узловых чисел.

Каноническим примером непозиционной системы счисления всегда приводится римская система счисления. В качестве узловых цифр здесь применялись заглавные буквы латинского алфавита:

I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000

Например, II = 1 + 1 = 2 здесь символ I обозначает единицу независимо от места в числе.

Однако римская система не может быть полностью непозиционной, так как меньшая цифра, которая стоящая слева перед большей, должна вычитаться из неё:

IV = 4, в то время как: VI = 6

Непозиционной системой счисления являлась и кириллическая система счисления — система счисления, применяемая на территории Древней Руси до XVIII века, основанная на алфавитной записи чисел с использованием кириллицы.

Что такое системы счисления

Системой счисления называется система записи чисел с помощью знаков по определенным правилам.

Символы, с помощью которых записываются числовые значения, обычно называют цифрами, а все вместе знаки системы счисления образуют алфавит. Количество знаков, используемых для обозначения чисел, называется основанием системы счисления.

Приведем примеры чисел систем счисления с различным основанием.

Основная десятичная система, привычная и общеупотребимая, имеет десять символов для обозначения всех чисел, то есть ее основание равно 10. Символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 представляют собой цифры. После цифры 9 в числовом ряду идет двузначное 10. При этом происходит сдвиг разрядной сетки числа влево на один разряд.

Десятичная система использует арабские цифры. Предположительно арабская система записи чисел возникла в Индии. Индийскую систему записи чисел описал Аль Хорезми в своем трактате «Об индийском счете».

Рис. 1. Портрет Аль Хорезми.

Системы счисления в информатике не ограничиваются применением десятичных цифр, самыми распространенными системами являются двоичная, восьмеричная и шестнадцатеричная системы счисления.

В двоичной системе счисления все просто. Основание равно 2. Обозначение чисел выполняется только двумя символами 0 и 1.

Восьмеричная система использует 8 знаков для обозначения чисел: 0, 1, 2, 3, 4, 5, 6, 7

И числовой ряд восьмеричных чисел выглядит так: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12 … Следует обратить внимание, что после 7 идет двузначное число 10, так как знаков всего восемь и происходит сдвиг разрядной сетки

Шестнадцатеричная система имеет основание 16. Она применяет в качестве символов арабские цифры от 0 до 9 и затем буквы латинского алфавита A, B, C, D, E, F. В числовом ряду шестнадцатеричных чисел после 9 идет А, а после F идет 10.

Тогда возникает вопрос, как определить, в какой системе счисления, например число 107. Цифры 0, 1, 7 используются как в восьмеричной, так и в десятичной и шестнадцатеричной системе счисления. Для того чтобы различать системы, существует специальное обозначение систем счисления. Числа помечаются индексом с основанием системы. Так, 107₈ – это восьмеричное число, 107₁₀ – десятичное число, 107₁₆ – шестнадцатеричное число.

в истории существуют примеры использования и других систем счисления. Так, некоторые коренные культуры Африки и Австралии используют двоичные и троичные системы. Индейцы Юки пользуются четверичной системой счисления, пятеричная система счисления распространена больше (по количеству пальцев на руке), ее элементы встречаются у древних персов и ацтеков, у индейцев племени Таманакос. У древних Шумеров использовалась шестидесятеричная система счисления, разбивка часа на 60 минут и минуты на 60 секунд, вероятно, отголоски этой системы.

Двоичная (бинарная) система счисления

Двоичная (или бинарная) система счисления — это позиционная система счисления с основанием 2.

Принцип считать двумя цифрами берёт своё начало ещё в Древнем Китае. Но развитие современной бинарной системы началось в XVII веке, а применение нашлось только в середине XX века.

История двоичной системы счисления

В 1605 году английский астроном и математик Томас Хэрриот описал двоичное представление чисел, а философ Фрэнсис Бэкон создал шифр из двух символов — A и B.

В 1670 году испанский богослужитель Хуан Карамюэль-и-Лобковиц опубликовал представление чисел в разных системах счисления, в том числе и двоичной.

Но самым значительным событием стали работы немецкого математика Готфрида Лейбница, который в 1703 году описал двоичную арифметику — математические операции с двоичными числами.

В 1838 году американский изобретатель Сэмюэл Морзе создал одноимённый шифр, содержащий два символа: «точка» и «тире». Их можно было передавать по телеграфу в виде длинных и коротких сигналов. Азбука Морзе не была бинарной системой в строгом смысле слова, но двоичный принцип впервые показал свою значимость.

В 1847 английский математик Джордж Буль изобрёл «булеву алгебру», в которой было два понятия («ложь» и «истина»), а также ряд логических законов.

В 1937 году американский инженер Клод Шеннон объединил бинарный принцип, булеву логику и электрические схемы и ввёл понятие «бит» — минимальное количество информации:

•  — ложь — нет тока (0 бит);
• 1 — истина — есть ток (1 бит).

С тех пор двоичную (бинарную) систему счисления стали использовать все ЭВМ, в том числе и современные компьютеры.

Числа в двоичной системе счисления

Двоичное число — это число, состоящее из двоичных цифр. А у нас их всего две. Принято обозначать и 1, но, как показала практика, это могут быть и два разных значения: «лампа горит» и «лампа не горит», «ток» и «нет тока» и так далее.

В следующей таблице приведены числа в двоичной системе (зелёный столбец) и соответствующие им числа в других часто используемых системах счисления — восьмеричной, десятичной и шестнадцатеричной.

Изображение: Лев Сергеев для Skillbox Media

Преимущества и недостатки двоичной (бинарной) системы счисления

Явные минусы двоичной системы обусловлены тем, что на интуитивном уровне людям она чужда — в отличие, например, от десятичной. И это — первый недостаток. Пройдёмся по остальным:

Длинная запись, неудобство с большими числами. Возьмём, к примеру, обозначение белого цвета в RGB-палитре: 25510, 25510, 25510 (здесь и далее нижний индекс указывает основание системы — двоичная, десятичная и так далее). Значения цветов принято записывать в шестнадцатеричной системе счисления (FF16, FF16, FF16). Если перевести это в бинарный вид, получится громоздко и непонятно:

Изображение: Лев Сергеев для Skillbox Media

• Долгое время ручных вычислений.
• Не применяется в повседневной жизни (если, конечно, вы не компьютер).

А вот для ЭВМ бинарочка — как родная. И отсюда следуют её плюсы:

• Позиционная система, имеет разряды.
• Применимы арифметические действия.
• Можно построить логику.
• Подходит для шифровки данных.
• Родной язык компьютерных систем.

Непозиционная система счисления

Для такой системы счисления количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.

Примерно в III тысячелетии до н.э. древние египтяне разработали десятичную непозиционную систему счисления, в которой для обозначения узловых чисел 1, 10, 100 использовались символы – иероглифы.

В большинстве непозиционных систем счисления новые числа образуются путём сложения узловых чисел.

Каноническим примером непозиционной системы счисления всегда приводится римская система счисления. В качестве узловых цифр здесь применялись заглавные буквы латинского алфавита:

I = 1,
V = 5,
X = 10,
L = 50,
C = 100,
D = 500,
M = 1000

Например, II = 1 + 1 = 2
здесь символ I обозначает единицу независимо от места в числе.

Однако римская система не может быть полностью непозиционной, так как меньшая цифра, которая стоящая слева перед большей, должна вычитаться из неё:

IV = 4, в то время как:
VI = 6

Непозиционной системой счисления являлась и кириллическая система счисления — система счисления, применяемая на территории Древней Руси до XVIII века, основанная на алфавитной записи чисел с использованием кириллицы.

Единичные непозиционные системы счисления

Единичные системы счисления с весовыми функциями (коэффициентами) f=b независящими от положения цифр являются (непоместными). Числа в них могут быть записаны в виде:, где:n — число цифр (единиц),k — число, порядковый номер цифры (единицы) в числе x_1,b,a — число, определяющее множество из которого берутся a_k,a_k — числа из одноэлементного множества a={1} (единицы),b — число, основание весовой функции,при b=1 веса всех цифр одинаковые и равны «1», при b≠1 веса всех цифр одинаковые и равны b.Так как весовой коэффициент — b может быть любым, то число единичных непозиционных систем счисления бесконечно. Наибольшее распространение получила единичная непозиционная система счисления с весовым коэффициентом равным единице (b=1). В народе иногда применяется единичная непозиционная система счисления с весовым коэффициентом равным двум (b=2), при счёте па́рами.

Из комбинаторики известно, что число записываемых кодов не зависит от основания весового коэффициента — b, который определяет диапазон представляемых числами x_1,b величин, и равно числу :, где:a=1 — одноэлементное множество a={1} из которого берутся цифры a_k, n — число элементов (цифр) в числе x_1,b. Из этого следует, что вышеприведённая запись для фиксированного числа разрядов — n определяет одно число.Сумма таких записей с числом разрядов n от 1 до n определяет n единичных чисел.

Как работает унарная система счисления?

Унарная система счисления основана на использовании только одного символа или цифры для представления чисел. В унарной системе счисления каждая цифра представляет единицу или одно количество. Это означает, что каждое число представляется повторением этой цифры определенное количество раз.

Например, в унарной системе счисления число 3 будет представлено как “111”, где каждая единица представляет одну единицу или одно количество. А число 5 будет представлено как “11111”.

Операции сложения, вычитания, умножения и деления в унарной системе счисления выполняются путем повторения соответствующих цифр определенное количество раз. Например, для сложения двух чисел в унарной системе счисления, мы просто объединяем их цифры вместе.

Например, чтобы сложить число 3 и число 5 в унарной системе счисления, мы просто объединяем их цифры и получаем “111111”.

Однако, из-за своей простоты, унарная система счисления неэффективна для представления больших чисел. Каждое число требует много символов для представления, что делает операции сложения, вычитания, умножения и деления очень трудоемкими и неэффективными.

Поэтому унарная система счисления обычно используется только для простых задач, где требуется представление количества или для теоретических исследований.

Позиционная система счисления

В позиционной системе счисления, количественный эквивалент цифры как раз зависит от её положения в записи числа. Основание позиционной системы счисления соответствует количеству цифр, которые составляют её алфавит.

Основным примером позиционной системы счисления является десятичная система записи чисел, к которой мы все так уже привыкли с детства, и в которой производим все основные математические вычисления.

Основанием позиционной системы счисления является любое натуральное число q>1. Алфавитом произвольной позиционной системы счисления с основанием q служат числа 0,1. q−1, каждое из которых записывается при помощи одного уникального символа; младшей цифрой всегда выступает 0.

Основными преимуществами любой позиционной системы счисления являются простота выполнения арифметических операций и небольшое количество символов, используемых в записи чисел.

Единичная непозиционная система счисления с единичным весовым коэффициентом

Целые числа записываются в виде:, где:a_k — единицы.

Особенностью такой системы является то, что если приписать к числу одну «цифру» (единицу), то число увеличивается лишь на эту единицу.(Для сравнения: если в обычной десятичной системе счисления к натуральному числу приписать справа 1, число увеличивается сразу в 10 раз — и плюс 1).

Поэтому такая система записи чисел обычно применяется там, где идёт последовательное увеличение подсчитываемой величины, например: при счёте числа дней, количества одинаковых событий и т. п.

Вероятно, подобная система является древнейшей системой счисления в истории человечества, для примера можно привести Московский математический папирус, датируемый приблизительно 1850 до н. э.

Дробные числа записываются в виде дроби из двух целых чисел: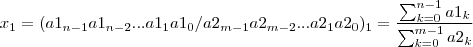, где:n — число цифр числителя (a1) дробного числа x₁,m — число цифр знаменателя (a2) дробного числа x₁.

Представление числа в позиционной системе счисления

В позиционной системе счисления с основанием q всякое число может быть представлено по формуле (развёрнутая форма записи):

Свёрнутой формой записи числа называется его представление в виде:

2⋅10 4 +1⋅10 3 +4⋅10 2 +6⋅10 1 +6⋅10 0 +1⋅10 −1 +2⋅10 −2 .

Десятичная система счисления, несмотря на свою универсальность, имеет большой недостаток — она избыточна, так как имеет большой алфавит. Для компьютерной техники наиболее удобной оказалась двоичная система счисления, поэтому мы рассмотрим её в следующем уроке.

2013-2020 Информатика. Полезные материалы по информационным технологиям. Использование материалов без активной ссылки на сайт запрещено! Публикация в печати только с письменного разрешения администрации.

Здравствуйте, в этой статье пойдет речь про унарную систему счисления. Ниже мы разберем основные определения, касающиеся данной темы, историю происхождения, её достоинства и недостатки. Рассмотрим области, где применяется эта система исчисления, примеры и её значение в информатике и других прикладных науках.

Урок 2. Общие сведения о системах счисления

С древних времен в практической деятельности человека часто возникала потребность счета и измерения. Результаты счета предметов выражались вначале весьма примитивно: зарубки на палочках, узелки на веревках и др. С развитием письменности человек начал отображать с помощью знаков (записывать) информацию о количестве предметов на подручных материалах: глиняных табличках, папирусе, бересте и др. Таким образом, для обозначения чисел стали использовать знаки.

Система
счисления — это
знаковая система, в которой приняты определённые правила записи чисел.

Цифры —
знаки, при помощи которых записываются числа.

Алфавит
системы счисления — совокупность цифр.

Одной из наиболее древних являлась египетская иероглифическая система счисления. В ней числа представлялись в виде отдельных знаков, например:
 

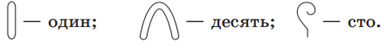
Так, число означало:

100+10+10+1+1+1=123

Существовали системы счисления, в которых для записи чисел использовались буквы алфавита, например старославянская система счисления.

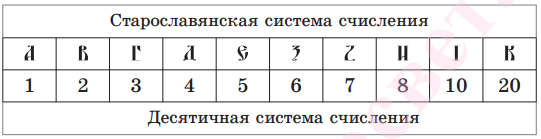
Десятичная система счисления зародилась в Индии приблизительно в 5 в., затем она появилась в арабских рукописях. Из арабских рукописей эта система пришла в Европу в 9-12 вв. Поэтому современную десятичную систему счисления называют арабской.

В любой системе счисления цифры служат для обозначения чисел, называемых узловыми; остальные числа (алгоритмические) получаются в результате каких-либо операций из узловых чисел.

Пример:
У вавилонян узловыми являлись числа 1 , 10, 60; в римской системе счисления узловые числа — это 1 , 5, 10, 50, 100, 500 и 1000, обозначаемые соответственно I, V, X, L, C, D, M.

Системы счисления различаются выбором узловых чисел и способами образования алгоритмических чисел. Можно выделить следующие виды систем счисления:

• унарная система;
• непозиционные системы;
• позиционные системы.

Простейшая и самая древняя система — так называемая унарная система счисления.

В ней для записи любых чисел используется всего один символ — палочка, узелок, зарубка, камушек. Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта.

Унарную систему ещё называют системой бирок.

Непозиционными называются такие системы счисления, в которых каждый знак (цифра) в записи любого числа имеет одно и то же значение и не зависит от своего расположения в числе.

В большинстве непозиционных систем счисления числа образуются путём сложения узловых чисел.

В непозиционной римской системе счисления для обозначения чисел используются следующие знаки:

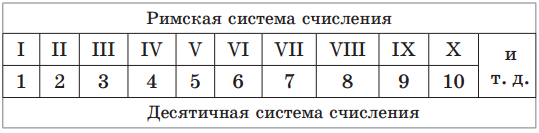
Например, число , записанное в римской системе счисления, в десятичной системе счисления означает: 10+10+5+1+1+1=28

Древнеегипетская и старославянская система также являются непозиционными.

Позиционными называют такие системы счисления, в которых значение каждого знака (цифры) в записи любого числа зависит от расположения (позиции) этого знака в числе. 

Количество цифр, используемых для записи чисел в позиционной системе
счисления, называется ее основанием.

Мы используем позиционную десятичную систему счисления. Основанием этой системы является число 10.

Для записи любого числа в десятичной системе счисления используют десять цифр: 0,1, 2, 3, 4, 5, 6, 7, 8, 9. Комбинируя эти цифры, можно записывать любые числа.

Например, цифры числа 737 в десятичной системе счисления являются коэффициентами его записи в виде суммы степенней числа 
 \( 737=7 \cdot10^2+3 \cdot10^1+7 \cdot10^0=7 \cdot100+3 \cdot10+7 \cdot1 \)

Из этого примера видно, что цифра 7 в зависимости от своей позиции в этом числе означает и 7 сотен, и 7 единиц, а цифра 3 три десятка.

Пример:

Рассмотрим десятичное число 13456,7. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме
переходим к развернутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:

\( 1⋅10^4+3⋅10^3+4⋅10^2+5⋅10^1+6⋅10^0+7⋅10^{−1} . \)

Последнее изменение: Воскресенье, 17 Сентябрь 2023, 20:20

Единичные позиционные системы счисления[]

Если весовые коэффициенты b зависят от положения цифр (единиц) (b(k)=f(k)), то единичная система счисления является поместной (позиционной). Целое число в ней может быть записано в виде:x1,b=(an−1an−2…a2a1a)1,b=∑k=n−1akbk{\displaystyle x_{1,b}=(a_{n-1}a_{n-2}…a_{2}a_{1}a_{0})_{1,b}=\sum _{k=0}^{n-1}a_{k}b_{k}}, где:

b_k=f(k) — числа весовой функции, весовые коэффициенты, зависящие от места (номера) цифры (единицы) в числе x_1,b.
Пример: при b_k=(k+1)
число 1₁ = 1*1 = 1₁₀,
число 11₁ = 1*2 + 1*1 = 3₁₀,
число 111₁ = 1*3 + 1*2 + 1*1 = 6₁₀,
число 1111₁ = 1*4 + 1*3 + 1*2 + 1*1 = 10₁₀.

При b_k=f(k)=1 единичная система счисления может рассматриваться и как вырожденная поместная (позиционная) положительная целочисленная система счисления с основанием равным 1.

При межразрядной функции f(k)=b(k)=bk образуются сдвоенные единичные показательные системы счисления:x1,b=(an−1an−2…a2a1a)1,b=∑k=n−1akbk{\displaystyle x_{1,b}=(a_{n-1}a_{n-2}…a_{2}a_{1}a_{0})_{1,b}=\sum _{k=0}^{n-1}a_{k}b^{k}}, в которых множество a{1}, из которого берутся a_k, равно 1, а основание межразрядной показательной функции не равно 1 (b≠1).
Дробные числа записываются в виде:x1,b=(an−1an−2…a1a,a−1a−2…a−(m−1)a−m)1,b=∑k=mn−1akbk{\displaystyle x_{1,b}=(a_{n-1}a_{n-2}…a_{1}a_{0},a_{-1}a_{-2}…a_{-(m-1)}a_{-m})_{1,b}=\sum _{k=m}^{n-1}a_{k}b^{k}}, где:m — число цифр дробной части числа x_1,b.

Единичные непозиционные системы счисления

Единичные системы счисления с весовыми функциями (коэффициентами) f=b, независящими от положения цифр, являются непозиционными (непоместными). Числа в них могут быть записаны в виде:

,

Поскольку весовой коэффициент b может быть любым, число единичных непозиционных систем счисления бесконечно. Наибольшее распространение получила единичная непозиционная система счисления с весовым коэффициентом, равным единице (b=1). В народе иногда применяется единичная непозиционная система счисления с весовым коэффициентом, равным двум (b=2) — при счёте па́рами.

Из комбинаторики известно, что число записываемых кодов не зависит от основания весового коэффициента — b, который определяет диапазон представляемых числами x_1,b величин, и равно числу размещений с повторениями:

,

a=1 — одноэлементное множество a= из которого берутся цифры a_k, :n — число элементов (цифр) в числе x_1,b.

Из этого следует, что вышеприведённая запись для фиксированного числа разрядов — n определяет одно число. Сумма таких записей с числом разрядов n от 1 до n определяет n единичных чисел.

Единичная непозиционная система счисления с единичным весовым коэффициентом[]

Целые числа записываются в виде:x1=(an−1an−2…a2a1a)1=∑k=n−1ak{\displaystyle x_{1}=(a_{n-1}a_{n-2}…a_{2}a_{1}a_{0})_{1}=\sum _{k=0}^{n-1}a_{k}}, где:a_k — единицы.

Особенностью такой системы является то, что если приписать к числу одну «цифру» (единицу), то число увеличивается лишь на эту единицу.(Для сравнения: если в обычной десятичной системе счисления к натуральному числу приписать справа 1, число увеличивается сразу в 10 раз — и плюс 1).

Поэтому такая система записи чисел обычно применяется там, где идёт последовательное увеличение подсчитываемой величины, например: при счёте числа дней, количества одинаковых событий и т. п.

Вероятно, подобная система является древнейшей системой счисления в истории человечества, для примера можно привести Московский математический папирус, датируемый приблизительно 1850 до н. э.

Дробные числа записываются в виде дроби из двух целых чисел:x1=(a1n−1a1n−2…a11a1a2m−1a2m−2…a21a2)1=∑k=n−1a1k∑k=m−1a2k{\displaystyle x_{1}=(a1_{n-1}a1_{n-2}…a1_{1}a1_{0}/a2_{m-1}a2_{m-2}…a2_{1}a2_{0})_{1}={\frac {\sum _{k=0}^{n-1}a1_{k}}{\sum _{k=0}^{m-1}a2_{k}}}}, где:n — число цифр числителя (a1) дробного числа x₁,m — число цифр знаменателя (a2) дробного числа x₁.