Урок 1: системы счисления

Введение

На
протяжении всей жизни мы сталкиваемся с числами и выполняем с ними
арифметические операции. Это нас не удивляет. Мы принимаем это как факт. И
откуда взялись цифры и результат? Что такое цифровая система? Где мы теперь с
ними встретимся? Мне было очень интересно, поэтому я решил изучить этот
предмет.

Эта
тема интересна и для меня, так как двоичная система счисления в настоящее время
стала очень важной в связи с ее использованием в электронных компьютерах.
Численные системы с базами 8 и 16 используются в программировании различных
процессов на компьютерах. Я
поставил перед собой цель: познакомиться с историей возникновения счетных и
числовых систем, изучить числовые системы, используемые в вычислениях,
позиционные и непозиционные числовые системы, а также арифметические действия в
различных системах

В данной диссертации рассматриваются различные
вычислительные системы

Я
поставил перед собой цель: познакомиться с историей возникновения счетных и
числовых систем, изучить числовые системы, используемые в вычислениях,
позиционные и непозиционные числовые системы, а также арифметические действия в
различных системах. В данной диссертации рассматриваются различные
вычислительные системы.

Слайд 9История возникновения и развития систем счисленияДвадцатеричная система счисления У ацтеков и

майя — народов, населявших в течение многих столетий обширные области

Американского континента и создавших там высочайшую культуру, в том числе и математическую, была принята двадцатеричная система счисления. Также двадцатеричная система счисления была принята и у кельтов, населявших Западную Европу начиная со II тысячелетия до нашей эры. Основу для счета в этой системе счисления составляли пальцы рук и ног. Некоторые следы двадцатеричной системы счисления кельтов сохранились во французской денежной системе: основная денежная единица, франк, делится на 20 (1 франк = 20 су).

К оглавлению

3.6 Славянская кириллическая десятеричная алфавитная

Эта нумерация была создана вместе со славянской алфавитной системой для перевода священных библейских книг для славян греческими монахами братьями Кириллом и Мефодием в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. До XVII века эта форма записи чисел была официальной на территории современной России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.

Числа записывали из цифр так же слева, направо, от больших к меньшим. Числа от 11 до 19 записывались двумя цифрами, причем единица шла перед десятком:

Читаем дословно «четырнадцать» — «четыре и десять». Как слышим, так и пишем: не 10+4, а 4+10, — четыре и десять. Числа от 21 и выше записывались наоборот, сначала писали знак полных десятков.

Запись числа, использованная славянами аддитивная, то есть в ней используется только сложение:

= 800+60+3

Для того чтобы не перепутать буквы и цифры, использовались титла — горизонтальные черточки над числами, что мы видим на рисунке.

Для обозначения чисел больших, чем 900 использовались специальные значки, которые дорисовывались к букве. Так образовывались числа:

	Тысяча	1000
	Тьма	10 000
	Легион	100 000
	Леодр	1 000 000
	Ворон	10 000 000
	Колода	100 000 000

Славянская нумерация просуществовала до конца XVII столетия, пока с реформами Петра I в Россию из Европы не пришла позиционная десятичная система счисления.

3.3 Древнегреческая аттическая пятеричная

В древнейшее время в Греции была распространена так называемая Аттическая система счисления, название происходит от области Греции – Аттики со столицей Афины.

В этой системе числа 1, 2, 3, 4 изображались соответствующим количеством вертикальных полосок: , , , . Число 5 записывалось знаком (древнее начертание буквы «Пи», с которой начиналось слово «пять» — «пенте»). Числа 6, 7, 8, 9 обозначались сочетаниями этих знаков:

Число 10 обозначалось — заглавной «Дельта» от слова «дека» — «десять». Числа 100, 1 000 и 10 000 обозначались H, X, M. Числа 50, 500, 5 000 обозначались комбинациями чисел 5 и 10, 5 и 100, 5 и 1 000, а именно:

Числа в пределах первого десятка тысяч записывались так:

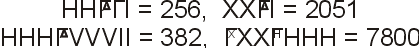
Двоичная (бинарная) система счисления

Двоичная (или бинарная) система счисления — это позиционная система счисления с основанием 2.

Принцип считать двумя цифрами берёт своё начало ещё в Древнем Китае. Но развитие современной бинарной системы началось в XVII веке, а применение нашлось только в середине XX века.

История двоичной системы счисления

В 1605 году английский астроном и математик Томас Хэрриот описал двоичное представление чисел, а философ Фрэнсис Бэкон создал шифр из двух символов — A и B.

В 1670 году испанский богослужитель Хуан Карамюэль-и-Лобковиц опубликовал представление чисел в разных системах счисления, в том числе и двоичной.

Но самым значительным событием стали работы немецкого математика Готфрида Лейбница, который в 1703 году описал двоичную арифметику — математические операции с двоичными числами.

В 1838 году американский изобретатель Сэмюэл Морзе создал одноимённый шифр, содержащий два символа: «точка» и «тире». Их можно было передавать по телеграфу в виде длинных и коротких сигналов. Азбука Морзе не была бинарной системой в строгом смысле слова, но двоичный принцип впервые показал свою значимость.

В 1847 английский математик Джордж Буль изобрёл «булеву алгебру», в которой было два понятия («ложь» и «истина»), а также ряд логических законов.

В 1937 году американский инженер Клод Шеннон объединил бинарный принцип, булеву логику и электрические схемы и ввёл понятие «бит» — минимальное количество информации:

— ложь — нет тока (0 бит);
1 — истина — есть ток (1 бит).

С тех пор двоичную (бинарную) систему счисления стали использовать все ЭВМ, в том числе и современные компьютеры.

Числа в двоичной системе счисления

Двоичное число — это число, состоящее из двоичных цифр. А у нас их всего две. Принято обозначать и 1, но, как показала практика, это могут быть и два разных значения: «лампа горит» и «лампа не горит», «ток» и «нет тока» и так далее.

В следующей таблице приведены числа в двоичной системе (зелёный столбец) и соответствующие им числа в других часто используемых системах счисления — восьмеричной, десятичной и шестнадцатеричной.

Изображение: Лев Сергеев для Skillbox Media

Преимущества и недостатки двоичной (бинарной) системы счисления

Явные минусы двоичной системы обусловлены тем, что на интуитивном уровне людям она чужда — в отличие, например, от десятичной. И это — первый недостаток. Пройдёмся по остальным:

Длинная запись, неудобство с большими числами. Возьмём, к примеру, обозначение белого цвета в RGB-палитре: 25510, 25510, 25510 (здесь и далее нижний индекс указывает основание системы — двоичная, десятичная и так далее). Значения цветов принято записывать в шестнадцатеричной системе счисления (FF16, FF16, FF16). Если перевести это в бинарный вид, получится громоздко и непонятно:

Изображение: Лев Сергеев для Skillbox Media

Долгое время ручных вычислений.
Не применяется в повседневной жизни (если, конечно, вы не компьютер).

А вот для ЭВМ бинарочка — как родная. И отсюда следуют её плюсы:

Позиционная система, имеет разряды.
Применимы арифметические действия.
Можно построить логику.
Подходит для шифровки данных.
Родной язык компьютерных систем.

Примеры алфавитного представления чисел в различных областях

2. В шестнадцатеричной системе счисления используются числа и буквы от A до F. Этот формат часто используется в программировании для представления цветов и адресов памяти. Например, число 255 в шестнадцатеричной системе будет обозначаться как FF.

3. В системе счисления с основанием 60, известной как секунды, представляются временные значения, такие как минуты и часы. В этой системе используются цифры от 0 до 9 и буквы от A до Z. Например, время 1 час 30 минут 45 секунд будет обозначаться как 1:30:45.

4. Арабские числа, которые мы используем в повседневной жизни, являются десятичной системой счисления, где используются цифры от 0 до 9. Это наиболее распространенная система счисления. Например, число 1234 в десятичной системе счисления будет обозначаться как 1234.

5. Римские цифры, которые используются в римской системе счисления, представляются буквами — I, V, X, L, C, D, M. Эта система счисления используется в основном для обозначения порядков и номеров, а не арифметических операций. Например, число 99 в римской системе будет обозначаться как XCIX.

Слайд 6Древнее изображение десятичных цифр не случайно: каждая цифра обозначает число

по количеству углов в ней. Например, 0 — углов нет,

1 — один угол, 2 — два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.Исторически десятичная система счисления сложилась и развивалась в Индии. Европейцы заимствовали индийскую тему счисления у арабов, назвав ее арабской, а исторически неправильное название удерживается и поныне. Возникновение и развитие десятичной системы счисления явилось одним из важнейших достижении человеческой мысли (наряду с появлением письменности). Однако десятичной системой счисления люди пользовались не всегда. В разные исторические периоды многие народы использовали другие системы счисления.

Системы счисления
анатомического происхождения

К оглавлению

Десятичная система счисления

Основой десятичной системы числа 10 является число 10, которое является единицей второй цифры, единицей третьей цифры будет 100 = 102, в общем случае единица каждой следующей цифры в десять раз больше, чем единица предыдущей цифры (предполагается, что выбор в качестве основы Д.С. числа 10 связан с подсчетом на пальцах).

Д. с. с. основывается на принципе позиции, т.е. в ней один и тот же символ (число) имеет различные значения в зависимости от того, где он находится. Поэтому только первые 10 номеров требуют специальных символов для покрытия всех номеров. Эти символы, которые обозначаются символами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называются цифрами. Для захвата числа вы определяете, сколько единиц высшей цифры в нем содержится; остальное определяется как количество единиц высшей цифры, на единицу меньше, и так далее. Полученные цифры записываются бок о бок: например, 4×102 + 7×101 + 3×100 = 473.

Таким образом, действия выполняются над числами в цифрах, т.е. отдельно над цифрами каждой цифры; если при этом числа складываются более чем до 10 (в случае сложения, умножения), то к следующей, более высокой цифре прибавляется одна или более единиц; в случае деления и вычитания, цифры должны быть разделены на более мелкие.

В современной жизни наиболее показательным вариантом использования системы непозиционного учета являются денежные отношения. Мы сталкиваемся с ними каждый день. Никому не приходит в голову, что сумма, которую мы тратим на еду в магазине, может зависеть от того, в каком порядке мы поставим монеты на стол. Номинальная стоимость монеты не зависит от порядка, в котором она была взята из кошелька. Это классический пример непозиционной системы подсчета.

Таким образом, в настоящее время система нумерации должностей является наиболее распространенной.

Непозиционные системы счисления

В настоящее время как позиционные, так и непозиционные системы расчета широко используются как в технологии, так и в быту.

В непозиционных системах нумерации вес фигуры не зависит от позиции, которую она занимает среди них. Примером непозиционной системы счисления является римская система счисления. Он появился в Древнем Риме и существует до сих пор. Традиционно используется для нумерации веков или для создания оглавления печатных произведений. Римские цифры можно найти на циферблатах часов.

Таким образом, в настоящее время система нумерации должностей является наиболее распространенной.

Рим. []

Римские обозначения чисел известны ныне лучше, чем любая другая древняя система счисления. Объясняется это не столько какими-то особыми достоинствами римской системы, сколько тем огромным влиянием, которым пользовалась римская империя в сравнительно недавнем прошлом. Этруски, завоевавшие Римскую империю в 7 в. до н.э., испытали на себе влияние восточно-средиземноморских культур. Этим отчасти объясняется сходство основных принципов Римской и аттической систем счисления. Обе системы были десятичными, хотя в обеих системах счисления особую роль играло число пять. Обе системы использовали при записи чисел повторяющиеся символы. Старыми римскими символами для обозначения чисел 1, 5, 10, 100 и 1000 были, соответственно, символы I, V, X, Q (или Е, или Д) и f. Хотя о первоначальном значении этих символов было написано много, их удовлетворительного объяснения у нас нет до сих пор. Согласно одной из распространенных теорий, римская цифра V изображает раскрытую руку с четырьмя прижатыми друг к другу пальцами и отставленным большим пальцем; символ X, согласно той же теории, изображает две скрещенные руки или сдвоенную цифру V. Символы чисел 100 и 1000, возможно, берут начало от греческих букв Q и f. Неизвестно, произошли ли более поздние обозначения C и M от старых римских символов или они акрофонически связаны с начальными буквами латинских слов, означавших 100 (центум) и 1000 (милле). Полагают, что римский символ числа 500, буква D, возник из половинки старого символа, обозначавшего 1000. Если не считать, что большинство римских символов скорее всего не были акрофоническими и что промежуточные символы для обозначения чисел 50 и 500 не были комбинациями символов чисел 5 и 10 или 5 и 100, то в остальном римская система счисления напоминала аттическую. Разумеется, в деталях они отличались. Римляне часто использовали принцип вычитания, поэтому иногда вместо VIIII использовали IX и XC вместо LXXXX; сравнительно позднее символ IV вместо IIII.

Дробей римляне избегали так же упорно, как и больших чисел. В практических задачах, связанных с измерениями, они не использовали дроби, подразделяя единицу измерения обычно на 12 частей, с тем чтобы результат измерения представить в виде составного числа, суммы кратных различных единиц, как это делается сегодня, когда длину выражают в ярдах, футах и дюймах. Английские слова «ounce» (унция) и «inch» (дюйм) происходят от латинского слова uncia (унция), обозначавшего одну двенадцатую основной единицы длины.

Алфавитное представление чисел: концепция и особенности

Основная идея алфавитного представления чисел состоит в том, чтобы повысить емкость системы счисления путём добавления дополнительных символов. В алфавитной системе счисления можно использовать цифры от 0 до 9 и дополнительные символы алфавита для обозначения бОльшего количества чисел.

Основными преимуществами алфавитного представления чисел являются:

Увеличение емкости системы счисления: добавление символов алфавита позволяет обозначать большее количество чисел.
Сокращение длины записи: использование символов алфавита вместо дополнительных цифр позволяет более компактно записывать числа.
Расширенные возможности: алфавитная система счисления позволяет вводить дополнительные символы и использовать их для обозначения специфических значений или предметов.

Однако, существуют и некоторые особенности алфавитного представления чисел. Например, при использовании символов алфавита может возникать перепутывание некоторых символов, особенно в случае схожих форм букв или цифр. Также, алфавитная система счисления может быть менее удобной для манипуляций с числами, так как требует знания и работы с дополнительными символами.

Список литературы

Фомин С. В. Системы счисления, 1988 г. Издание: Главная редакция физико-математической литературы издательства «Наука».
Гашков С. Б. Системы счисления и их применение, 2013 г. Издание: МЦНМО.
Ковриженко, Г.А. Системы счисления и двоичная арифметика, 1985 г.
Фринланд А.Я. Информатика. М., 2006.
Сидоров В.К. Системы счисления.//Наука и жизнь 2001. №2.
Радюк Л. Алгоритм перевода в двоичную и из двоичной системы счисления.// Наука и жизнь. 2006. №1.
Рассел Джесси — Двоичная система счисления, 2013 г. Издание: Книга по Требованию.
Колмогоров А.Н. Система счисления, 1971 г. Издательство «Академия Наук СССР».

Похожие рефераты:

Реферат на тему: Защитники отечества
Реферат на тему: Моделирование по информатике
Реферат на тему: Управление персоналом
Реферат на тему: Человек и природа
Реферат на тему: Зимние Олимпийские игры
Реферат на тему: Налоговая система РФ
Реферат на тему: Амурский тигр
Реферат на тему: Философия и религия
Реферат на тему: Искусство и власть
Реферат на тему: Птицы
Реферат на тему: Ураган
Реферат на тему: Правительство РФ

Основные системы алфавитной записи чисел

Греческая

Единицы	α	β	γ	δ	ε	ϝ	ζ	η	θ
1	2	3	4	5	6	7	8	9
Десятки	ι	κ	λ	μ	ν	ξ	ο	π	ϟ
10	20	30	40	50	60	70	80	90
Сотни	ρ	σ	τ	υ	φ	χ	ψ	ω	ϡ
100	200	300	400	500	600	700	800	900

Примечание 1. В византийские времена вместо дигаммы (ϝ) значение 6 стала выражать стигма (ϛ), лигатура букв сигма (σ) и тау (τ).

Примечание 2. Архаические буквы коппа (ϟ) и сампи (ϡ) не входят даже в классический 24-буквенный древнегреческий алфавит, но для записи чисел (имея значение 90 и 900, соответственно) изредка применяются до сих пор.

Кириллическая

Кириллическая система буква в букву воспроизводит греческую. В стандартном церковнославянском варианте, используемом и сегодня, она имеет следующий вид:

Единицы	а	в	г	д	є	ѕ	з	и	ѳ
1	2	3	4	5	6	7	8	9
Десятки	і	к	л	м	н	ѯ	ѻ	п	ч
10	20	30	40	50	60	70	80	90
Сотни	р	с	т	у	ф	х	ѱ	ѿ	ц
100	200	300	400	500	600	700	800	900

Кроме того, старинные варианты кириллической записи чисел могли отличаться следующим:

Тибетская

В Тибете для нумерации страниц и книг в библиотеках применяется тибетский алфавит. От 1 до 30 — простые буквы, от 31 до 60 — те же буквы с огласовкой гигу, от 61 до 90 — с огласовкой жабкью, от 91 до 120 — дренбу, от 121 до 150 — наро. Какая то подобная система применяется по-видимому и в тибетской астрологии карци.

Выбранная мною тема исследования привлекла меня возможностью узнать, как можно больше о появлении чисел и о том, какие еще были способы записи числовой информации.

Как мне кажется, выбранная мною тема может быть также интересна не только мне, но и моим сверстникам, поскольку алфавитные системы счисления стали основой для развития математики во многих странах и являются частью их богатой истории, в том числе частью истории нашей страны.

Вложение	Размер
lanin_matematika_5b.doc	149 КБ

1.1. Зарождение счета в глубокой древности

Наши первоначальные представления о числе и форме относятся к очень отдаленной эпохе древнего каменного века – палеолита. В течении сотен тысячелетий этого периода люди жили в пещерах, в условиях, мало отличавшихся от жизни животных, и их энергия уходила преимущественно на добывание пищи простейшим способом – собиранием её, где только это было возможно. Люди изготовляли орудия охоты и рыболовства, вырабатывали язык для общения друг с другом, а в эпоху позднего палеолита украшали своё существование, создавая произведения искусства, статуэтки и рисунки.

Пока не произошёл переход от простого собирания пищи к активному её производству, от охоты и рыболовства к земледелию, люди мало продвинулись в понимании числовых величин и пространственных отношений. Лишь с наступлением этого фундаментального перелома, переворота, когда пассивное отношение человека к природе сменилось активным, мы вступаем в новый каменный век, в неолит.

Самым трудным этапом, который прошло человечество при выработке понятия о числе, считается выделение им понятия единицы из понятия «много». Оно произошло, по всей вероятности, ещё тогда, когда человечество находилось на низшей ступени развития. В.В. Бобынин объясняет такое выделение тем, что человек обычно захватывает рукой один предмет, а это, по его мнению, и выделило единицу из множества. Таким образом, начало счисление Бобынин мыслит как создание системы, состоящей из двух представлений: единица и неопределенное множество. .

Так, например, племя ботокудов, жившее в Бразилии, выражало числа только словами «один» и «много». Появление элемента «два» объясняется выявлением возможности взять по одному предмету в каждую руку. На первоначальном этапе счёта человек связывал это понятие с понятием обеих рук, в которых находится по одному предмету в каждой. При выражении понятия «три» встретилось затруднение: у человека нет третьей руки; это затруднение было преодолено, когда человек догадался помещать третий предмет у своих ног. Таким образом, «три» характеризовалось поднятием обеих рук и указанием на ноги. Отсюда сравнительно характерно произошло выделение и понятие «четыре», так как с одной стороны, к этому побуждало сопоставление двух рук и двух ног, а с другой – возможность поместить по одному предмету у каждой ноги. На первой ступени развития счета человек еще отнюдь не пользовался наименованием чисел, а выражал их или у ног, или соответствующими телодвижениями или жестами.

Дальнейшее развитие счета относится, вероятно, к той эпохе, когда человечество ознакомилось с некоторыми формами производства – охотой и рыболовством. Человеку пришлось изготавливать простейшие орудия для овладения этими производствами. Кроме того, продвижение человека в холодные страны заставило его делать одежду и создавать орудия для обработки кожи.

Мало-помалу сложилось первобытно-коммунистическое общество с соответствующим распределением пищи, одежды и орудия. Все эти обстоятельства вынудили человека так или иначе вести счет общего имущества, сил врага, с которым приходилось вступать в борьбу за овладение новыми территориями. Процесс счета уже не мог остановиться на четырех и должен был развиваться далее и далее.

На этой ступени развития человек уже отказывается от необходимости брать пересчитываемые предметы в руку или класть к ногам. В математику входит первая абстракция, заключающаяся в том, что пересчитываемые предметы заменяются какими-либо другими однородными между собой предметами или знаками: камешками, узелками, ветками, зарубками. Операция производится по принципу взаимно-однозначного соответствия: каждому пересчитываемому предмету в соответствие один из предметов, выбранных в качестве орудия счета (то есть один камешек, один узелок на веревке и т.д.). Следы такого рода счета сохранились у многих народов и до настоящего времени. Иногда такие примитивные орудия счета (камешки, раковины, косточки) нанизывали на шнурок или палочку, чтобы не растерять. Это впоследствии привело к созданию более совершенных счётных приборов, сохранивших своё значение и до наших дней: русские счёты и сходный с ними китайский суан-пан.

Начало развития

Согласно истории человек быстро эволюционировал – изобретались новые орудия для охоты, и появлялись инструменты, которые помогали вести сельское хозяйство. В результате развития людское племя начало быстро отвоевывать земли у дикой природы. Количество добычи, как и население племен неуклонно росло. Человеку больше не хватало обозначений один, пара, несколько или много. Это привело к возникновению и созданию первой, самой древней в истории, простейшей формы счисления, называемой унарной (единичной).

В этой форме счисления алфавит состоял из одного символа. Древние люди использовали зарубки на дереве, либо наносили палочки на стены пещер и кости убитых животных. Сколько объектов могли подсчитывать древнейшие племена – неизвестно. Однако, в 1937 году в Вестонице учеными археологами была найдена волчья кость, на которую было поставлено пятьдесят пять насечек. На данный момент это наибольшее значение, которое удалось подтвердить.

Унарная форма используется и в современной истории – я думаю, что каждый из вас видел фильмы, где заключенные ставят палочки на стенах, обозначая количество дней, проведенных в неволе. Также применяется для обучения маленьких детей счету – вспомните про счетные палочки.

Что такое системы счисления

Системой счисления называется система записи чисел с помощью знаков по определенным правилам.

Символы, с помощью которых записываются числовые значения, обычно называют цифрами, а все вместе знаки системы счисления образуют алфавит. Количество знаков, используемых для обозначения чисел, называется основанием системы счисления.

Приведем примеры чисел систем счисления с различным основанием.

Основная десятичная система, привычная и общеупотребимая, имеет десять символов для обозначения всех чисел, то есть ее основание равно 10. Символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 представляют собой цифры. После цифры 9 в числовом ряду идет двузначное 10. При этом происходит сдвиг разрядной сетки числа влево на один разряд.

Десятичная система использует арабские цифры. Предположительно арабская система записи чисел возникла в Индии. Индийскую систему записи чисел описал Аль Хорезми в своем трактате «Об индийском счете».

Рис. 1. Портрет Аль Хорезми.

Системы счисления в информатике не ограничиваются применением десятичных цифр, самыми распространенными системами являются двоичная, восьмеричная и шестнадцатеричная системы счисления.

В двоичной системе счисления все просто. Основание равно 2. Обозначение чисел выполняется только двумя символами 0 и 1.

Восьмеричная система использует 8 знаков для обозначения чисел: 0, 1, 2, 3, 4, 5, 6, 7

И числовой ряд восьмеричных чисел выглядит так: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12 … Следует обратить внимание, что после 7 идет двузначное число 10, так как знаков всего восемь и происходит сдвиг разрядной сетки

Шестнадцатеричная система имеет основание 16. Она применяет в качестве символов арабские цифры от 0 до 9 и затем буквы латинского алфавита A, B, C, D, E, F. В числовом ряду шестнадцатеричных чисел после 9 идет А, а после F идет 10.

Тогда возникает вопрос, как определить, в какой системе счисления, например число 107. Цифры 0, 1, 7 используются как в восьмеричной, так и в десятичной и шестнадцатеричной системе счисления. Для того чтобы различать системы, существует специальное обозначение систем счисления. Числа помечаются индексом с основанием системы. Так, 107₈ – это восьмеричное число, 107₁₀ – десятичное число, 107₁₆ – шестнадцатеричное число.

в истории существуют примеры использования и других систем счисления. Так, некоторые коренные культуры Африки и Австралии используют двоичные и троичные системы. Индейцы Юки пользуются четверичной системой счисления, пятеричная система счисления распространена больше (по количеству пальцев на руке), ее элементы встречаются у древних персов и ацтеков, у индейцев племени Таманакос. У древних Шумеров использовалась шестидесятеричная система счисления, разбивка часа на 60 минут и минуты на 60 секунд, вероятно, отголоски этой системы.

Позиционные номера

В
системах подсчета позиций вес каждой цифры изменяется в зависимости от ее
положения в последовательности цифр, представляющих число. Каждая система
позиций характеризуется своей базой. Основой системы нумерации элементов
является количество различных символов или символов, используемых для
представления цифр в этой системе. Любое натуральное число — два, три, четыре,
шестнадцать и т.д. — может быть принято за основу. Следовательно, возможны
бесконечные системы позиций: двоичные, состоящие из чисел 0 и 1; троичные,
состоящие из чисел 0,1,2; и так далее.

Системы
позиционирования удобны тем, что позволяют захватывать большие числа с
небольшим количеством символов при выполнении простых и легко выполняемых
арифметических операций.

Позиционные системы счисления. Основные определения.

Система счисления или нумерация: способ записи чисел
Цифры: символы, при помощи которых записываются числа
Алфавит системы счисления: совокупность цифр, используемых в данной системе счисления
Размерность системы счисления: количество цифр в алфавите системы счисления
Позиционная система счисления: такая система счисления, в которой количественный эквивалент цифры зависит от ее положения в записи числа

Арабская десятичная система счисления является позиционной: значения цифр умножаются на “веса” соответствующих разрядов. Например, \(8347 = 8\cdot 1000 + 3\cdot 100 + 4\cdot 10 + 7\cdot 1\).

Базис позиционной системы счисления: Последовательность чисел, каждое из которых задает количественный эквивалент соответствующего разряда

Основным достоинством практически любой позиционной системы счисления является возможность записи любого числа при помощи конечного набора цифр.

Традиционная система счисления: позиционная система счисления, базис которой образуют члены геометрической прогрессии, а значения цифр есть целые неотрицательные числа

Базис десятичной системы счисления образуется геометрической прогрессией со знаменателем \(10\), двоичной и восьмеричной, соответственно, \(2\) и \(8\).

Основание традиционной системы счисления: знаменатель геометрической прогрессии, члены которой образуют базис системы счисления

Традиционные системы счисления иначе называют P-ичными. Например, двоичная, третичная, четвертичная, пятиричная, и т.п.

В P-ичных системах размерность алфавита равна основанию.

В качестве позиционных систем, не являющихся традиционными, можно привести фибоначчеву и факториальную системы счисления, а так же различные сбалансированные системы счисления. В рамках данного курса нас в основном интересуют традиционные системы счисления.

Основанием P-ичной системы счисления может быть любое натуральное число большее 1.

Для однозначного определения позиционной системы счисления необходимо и достаточно указать ее базис.

Для однозначного определения традиционной системы необходимо и достаточно указать ее основание.

Что касается алфавита систем счисления, условимся, что для первых 10 символов мы используем арабские цифры 0, 1, … 9. Для следующих – латинские буквы A, B, C, …, Z. Для всех остальных, если понадобится, будем указывать десятичный номинал числа в квадратных скобках, например, .